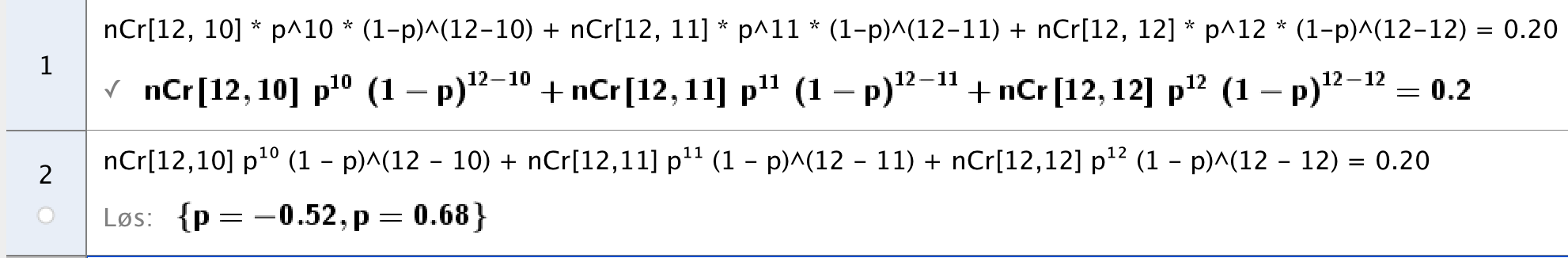Om vedkommende får gevinst for hver femte rekke, så må 5 * P(gevinst) = 1 som gir oss at P(gevinst) = 0,20.
Videre vet vi at vedkommende får gevinst ved tre tilfeller, 10, 11 eller 12 rette. Vi vet at P(10) + P(11) + P(12) = 0,20
For sannsynligheten for å ta rett på 10 kamper, blir det en bionomisk fordeling med n = 12 og r = 10, i formelen $nCr * p^r * (1-p)^{n-r}$
Her er det sannsynligheten p som er ukjent, resten vet vi. Jeg velger å bruke CAS for å løse denne:
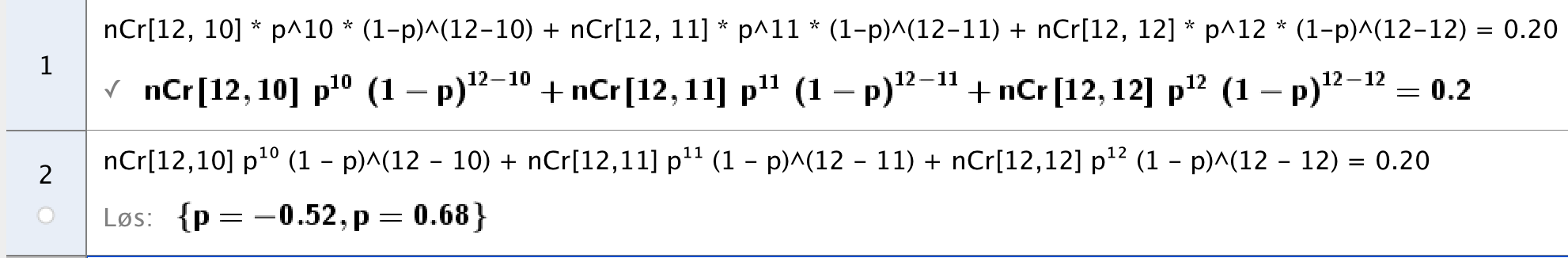
Ser da vekk fra den negative verdien, og får da at sannsynligheten for å tippe riktig på en kamp, er 0,68. Det er 35 prosentpoeng mer enn om man hadde brukt ren og skjær tipping (i det lange løp), gitt at det vedkommende hevder faktisk holder mål.