Page 1 of 1
Derivasjon, kjerneregelen
Posted: 05/03-2017 12:34
by TRCD
Hei. Har løst en en oppgave ved å bruke kjerneregelen og er ganske sikker på at jeg har fått riktig svar. I fasiten har de derimot forkortet/gjort uttrykket enklere, og jeg skjønner ikke helt hvordan de har kommet fram til det uttrykket.
Gjelder oppgave 5,54a
Man skal derivere: (x^2-5)^4 - (x^2-5)^3
Jeg fikk: 8x(x^2-5)^3 - 6x(x^2-5)^2
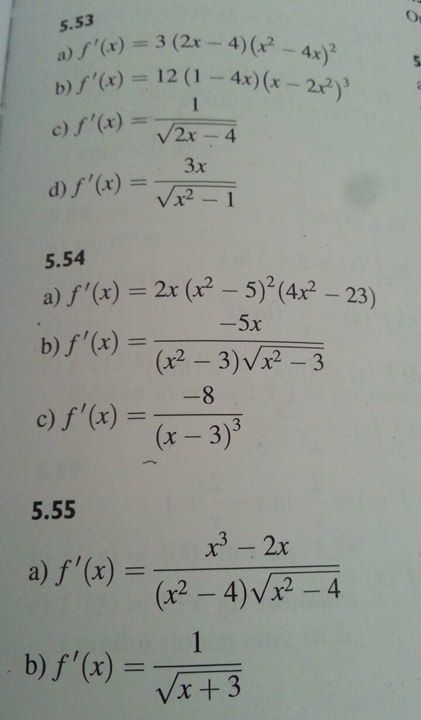
- 17160366_10202821450655521_1786420768_n.jpg (36.78 KiB) Viewed 1971 times
Re: Derivasjon, kjerneregelen
Posted: 05/03-2017 13:20
by DennisChristensen
Jeg klarer ikke å se hva du selv har fått som svar på oppgaven. Må nesten få sammenlikne svarene for å kunne hjelpe deg.
Re: Derivasjon, kjerneregelen
Posted: 05/03-2017 13:29
by TRCD
Man skal derivere: (x^2-5)^4 - (x^2-5)^3
Jeg fikk: 8x(x^2-5)^3 - 6x(x^2-5)^2
Re: Derivasjon, kjerneregelen
Posted: 05/03-2017 13:45
by DennisChristensen
TRCD wrote:Man skal derivere: (x^2-5)^4 - (x^2-5)^3
Jeg fikk: 8x(x^2-5)^3 - 6x(x^2-5)^2
Det er riktig, og du kan faktorisere videre. $2x\left(x^2-5\right)^2$ er en felles faktor i begge leddene, så vi kan faktorisere ut dette:
$8x(x^2-5)^3 - 6x(x^2-5)^2 = 2x\left(x^2 - 5\right)^2\left[4(x^2 - 5) - 3\right] = 2x\left(x^2 - 5\right)^2\left(4x^2 - 23\right).$
Re: Derivasjon, kjerneregelen
Posted: 05/03-2017 13:57
by TRCD
DennisChristensen wrote:TRCD wrote:Man skal derivere: (x^2-5)^4 - (x^2-5)^3
Jeg fikk: 8x(x^2-5)^3 - 6x(x^2-5)^2
Det er riktig, og du kan faktorisere videre. $2x\left(x^2-5\right)^2$ er en felles faktor i begge leddene, så vi kan faktorisere ut dette:
$8x(x^2-5)^3 - 6x(x^2-5)^2 = 2x\left(x^2 - 5\right)^2\left[4(x^2 - 5) - 3\right] = 2x\left(x^2 - 5\right)^2\left(4x^2 - 23\right).$
Takker
