matematikk.net

Har et tak som er 100m^2 med vinkel på 45 grader. På et døgn regner det 40mm regn. Regnet som renner på taket renner ned i en tønne med diameter på 1meter. Hvor høyt blir vannet i tønna det neste døgnet?

Noen som vet?

40mm=0.04m, så volumet av regnvannet blir vel $100\cdot \cos 45 \cdot 0.04 \text{m}^3$, der faktoren $\cos 45$ kommer av at man må ta hensyn til vinkelen på taket. (taket dekker $100\cdot \cos 45\text{m}^2$ på bakken)

Dette volumet blir i tønna lik $100\cdot \cos 45 \cdot 0.04 = \pi \cdot 0.5^2 \cdot h$ der $h$ er høyden på vannet i tønna.

Er det mulig å gjøre denne oppgaven uten cos?

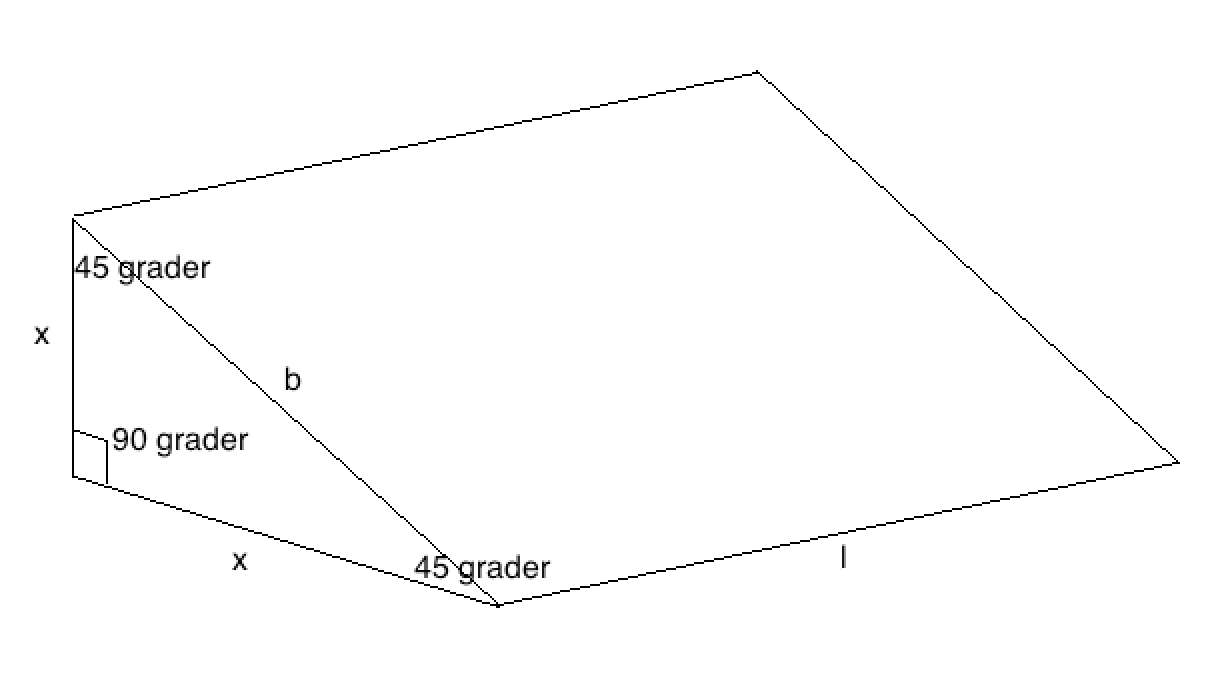
Ja, man kan jo også bruke pytagoras for å finne bredden på taket langs bakken. Vi får jo en likebeint, rettvinklet trekant som tverrsnittet på taket.

Okei, hvordan går man frem for å finne bredden på taket?

Pytagoras gir at $x^2+x^2=b^2$, så $b=\sqrt{2}x$.

Areal av taket er $100=b\cdot l$.

Arealet av området på bakken som er dekket av taket blir da $x\cdot l = \frac{1}{\sqrt{2}}b\cdot l = \frac{1}{\sqrt{2}}\cdot 100$.

Okei, så da får vi at området er 70,9m^2 når taket ligger flatt?

Så da vil det komme 40mm regn på det området. 40mm = 40 liter per m^2. Det blir da 40L*70,9 = 2836,9L vann på taket?

Hvordan kommer jeg så frem for å finne høyden i tønna?

Hvis vannet i tønna har høyden h, så vil dette tilsvare et volum på $\pi* 0.5^2 *h $ kubikkmeter. Dette må da settes lik det volumet du fant. Da får du en likning der høyden h er den ukjente. Det er trolig bedre å regne i kubikkmeter enn liter her.