Page 1 of 1
Andreordens diff.likning.
Posted: 11/04-2018 22:03
by Myron
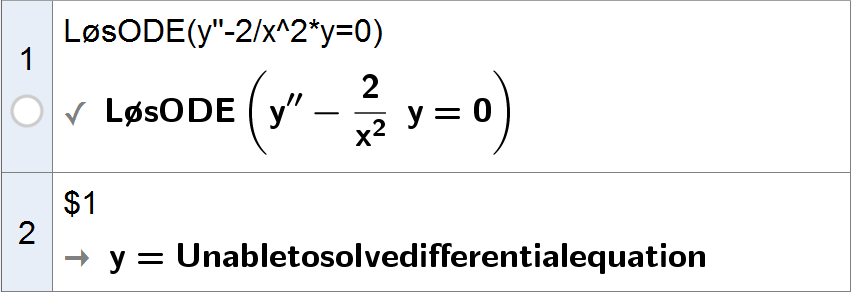
- Matte 7.png (22.19 KiB) Viewed 1571 times
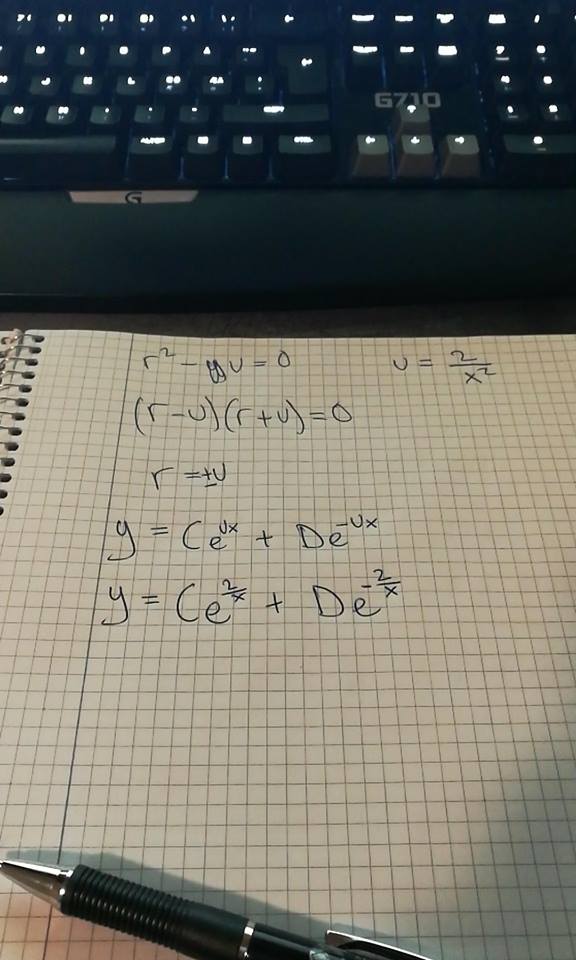
- Matte 8.jpg (64.66 KiB) Viewed 1571 times
Hei, har prøvd meg på denne diff.likningen. Føler at det her ble for lett, og lurer på hvordan man skal gjøre den.
Re: Andreordens diff.likning.
Posted: 12/04-2018 19:35
by Myron
Fant en skrivefeil. Skal være [tex](r-\sqrt{u})(r+\sqrt{u})=0[/tex]
Hvis jeg da går videre får jeg: [tex]y=C_1*e^{\sqrt{\frac{2}{x}}}+C_2*e^{\sqrt{-\frac{2}{x}}}[/tex].
Re: Andreordens diff.likning.
Posted: 12/04-2018 22:07
by Markus
Diff.likningen du presenterer kalles en Euler-Cauchy-likning. Det ser ut som at du har prøvd å løse diff.likningen med løsningsmetoden for andre ordens diff.likninger med konstante koeffisienter, men dette er ikke tilfellet her; $x^2$ er jo ikke konstant. Selv om det er en annen type likning er løsningsmetoden ganske lik som den du bruker i sammenheng med 2. ordens diff.likninger med konstante koeffisienter.
Diff.likningen er ekvivalent med $$x^2y'' - 2y = 0$$ Anta at $y=x^m$ er en løsning på diff.likningen. Da er $y''=m(m-1)x^{m-2}$, substituerer vi dette inn i likningen får vi $$x^2(m(m-1)x^{m-2}) - 2x^m = m(m-1)x^m - 2x^m = x^m(m^2-m-2) =0$$ Anta videre wlog at $x \neq 0$, da $\nexists m$ som er slik at $x^m=0$, og da må løsningen på den omformete diff.likningen være gitt ved $$m^2-m-2=0$$ Som har løsningsmengden $\{-1,2\}$. Substituerer vi nå tilbake ser vi at $$y_1= c_1 x^{-1} = \frac{c_1}{x} \qquad \text{og} \qquad y_2 = c_2x^2$$ er to spesielle løsninger på diff.likningen, så $$y=\frac{c_1}{x} + c_2x^2$$ er den generelle løsningen på diff.likningen.