Page 1 of 1
R2- Enhetsformel og vis med sinx og cosx
Posted: 12/09-2018 15:30
by anjafur
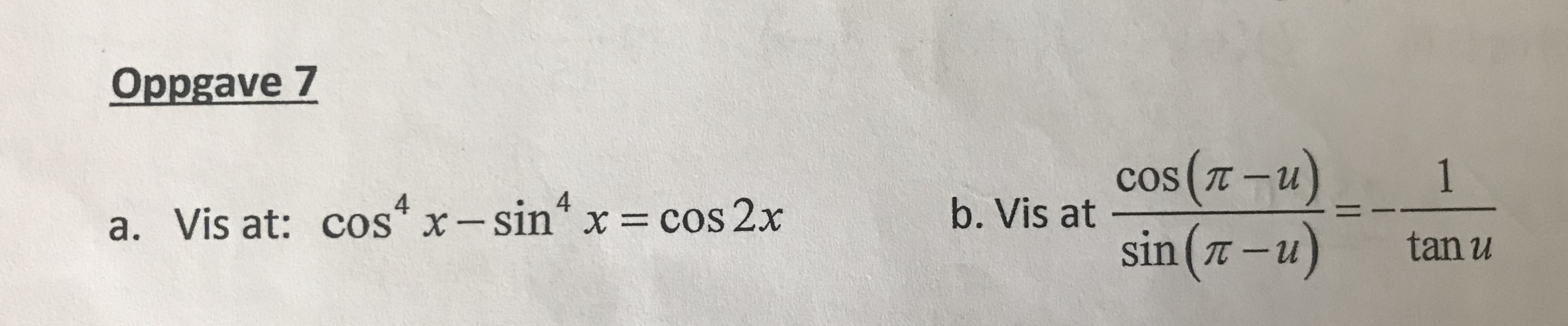
- B0F3E978-4FB6-4D59-9114-588F237B200A.jpeg (579.05 KiB) Viewed 1605 times
Hei, jeg vet ikke hva jeg skal gjøre på disse oppgavene.
Re: R2- Enhetsformel og vis med sinx og cosx
Posted: 12/09-2018 15:46
by Kay
anjafur wrote:B0F3E978-4FB6-4D59-9114-588F237B200A.jpeg
Hei, jeg vet ikke hva jeg skal gjøre på disse oppgavene.
Fra konjugatsetningen og cos^2(x)+sin^2(x)=1 får vi
[tex]\cos^4(x)-\sin^4(x)=(\cos^2(x)-\sin^2(x))(\cos^2(x)+\sin^2(x))=\cos^2(x)-\sin^2(x)=\cos(2x)[/tex]
Fra reglene om sin(u-v) og cos(u-v)
[tex]\frac{\cos(\pi-u)}{\sin(\pi-u)}=\frac{\cos(\pi)\cos(u)+\sin(\pi)\sin(u)}{\sin(\pi)\cos(u)-\sin(u)\cos(\pi)}=\frac{-\cos(u)}{\sin(u)}=-\frac{\cos(u)}{\sin(u)}=-\cot(u)=-\frac{1}{\tan(u)}[/tex]
Re: R2- Enhetsformel og vis med sinx og cosx
Posted: 12/09-2018 16:52
by anjafur
Kay wrote:anjafur wrote:B0F3E978-4FB6-4D59-9114-588F237B200A.jpeg
Hei, jeg vet ikke hva jeg skal gjøre på disse oppgavene.
Fra konjugatsetningen og cos^2(x)+sin^2(x)=1 får vi
[tex]\cos^4(x)-\sin^4(x)=(\cos^2(x)-\sin^2(x))(\cos^2(x)+\sin^2(x))=\cos^2(x)-\sin^2(x)=\cos(2x)[/tex]
Fra reglene om sin(u-v) og cos(u-v)
[tex]\frac{\cos(\pi-u)}{\sin(\pi-u)}=\frac{\cos(\pi)\cos(u)+\sin(\pi)\sin(u)}{\sin(\pi)\cos(u)-\sin(u)\cos(\pi)}=\frac{-\cos(u)}{\sin(u)}=-\frac{\cos(u)}{\sin(u)}=-\cot(u)=-\frac{1}{\tan(u)}[/tex]
Vi har ikke lært den regelen om sin(u-v) og cos(u-v).
Re: R2- Enhetsformel og vis med sinx og cosx
Posted: 12/09-2018 17:21
by Kay
Da skriver jeg de ned slik at du kan de til senere, formlene er essensielle.
[tex]\sin(u+v)=\sin(u)cos(v)+sin(v)cos(u)[/tex]
[tex]\sin(u-v)=\sin(u)\cos(v)-\sin(v)\cos(u)[/tex]
[tex]\cos(u+v)=\cos(u)\cos(v)-\sin(u)\sin(v)[/tex]
[tex]\cos(u-v)=\cos(u)\cos(v)+\sin(u)\sin(v)[/tex]
Disse må du nesten bare lære deg. Fra disse oppstår det også at;
[tex]\sin(\pi-u)=\sin(u)[/tex]
[tex]\cos(\pi-u)=-\cos(u)[/tex]
[tex]\sin(\pi + u)=-\sin(u)[/tex]
[tex]\cos(\pi+u)=-\cos(u)[/tex]