Page 1 of 1
Graf
Posted: 30/10-2018 16:01
by heimattehei

- Skjermbilde5.PNG (55.7 KiB) Viewed 1391 times
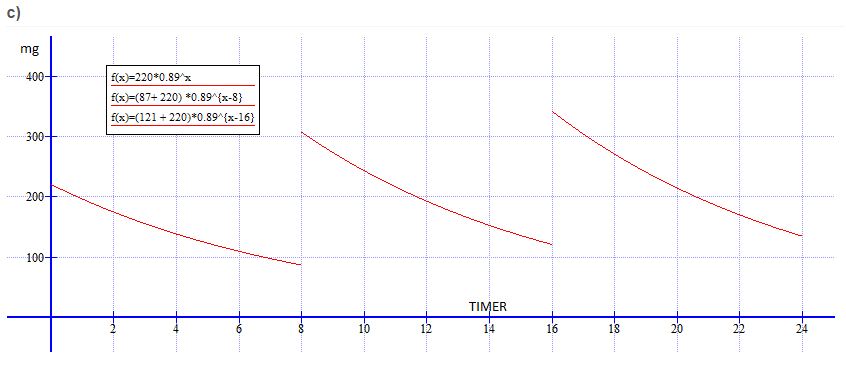
- Skjermbilde6.PNG (11.01 KiB) Viewed 1391 times
Hei!
Noen som kunne vært så snill å forklare oppgave c) der?
Forstår ikke helt hva de har gjort i geogebra og hvordan man kan skrive funksjonene inn
Kanskje noe med at jeg ikke forstår hva disse "parantesene" brukes til: { }
Re: Graf
Posted: 30/10-2018 16:42
by Guest
For å lage sånne grafer i Geogebra må du skrive:
Funksjon(Funksjonen du ønsker å vise, nedre grense, øvre grense)
F.eks. vil Funksjon(x, 1, 2) Vise grafen til f(x) = x mellom x=1 og x=2.
Hvis mengden med antibiotika reduseres med 11% i timen betyr det at du har en vekstfaktor på 1-0.11 = 0.89
Hvis du starter med 220mg vil du dermed ha
$220 \cdot 0.89$ etter 1 time
$220 \cdot 0.89^2$ etter 2 timer
$220 \cdot 0.89^3$ etter 3 timer
...
$220 \cdot 0.89^t$ etter t timer.
Etter t=8 timer har du dermed
$220 \cdot 0.89^8$ mg med antibiotika igjen i kroppen.
Når Vibeke tar en ny tablett etter 8 timer vil det fortsatt være igjen restene fra den forrige i tillegg til den nye tabletten.
Mengden med antibiotika vil dermed være $220 \cdot 0.89^8 + 220 = 306.6mg$ med en gang hun tar den nye tabletten. Så kan du begynne å telle fra start igjen. Etter t=2 timer fra hun tok den andre tabletten er det igjen $306.6 \cdot 0.89^2$.
Re: Graf
Posted: 31/10-2018 10:03
by heimattehei
Hei, og takk for svar.
Det jeg egentlig lurer på etter å ha prøvd meg litt frem er forklaringen på hvorfor 0.89 er opphøyd i x-8/x-16 alt etter hvor grafen skal starte (jf. oppg. C). Om man bare skriver inn funksjonene og nedre- og øvre grense av x-verdier vil det bli seende slik ut:
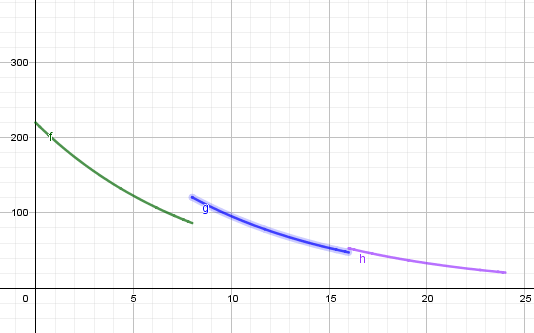
- Skjermbilde7.PNG (15.84 KiB) Viewed 1372 times
bilde 1
Så forstår det sånn at når vi opphøyer i x-8/x-16 så starter på en måte grafen på nytt der:
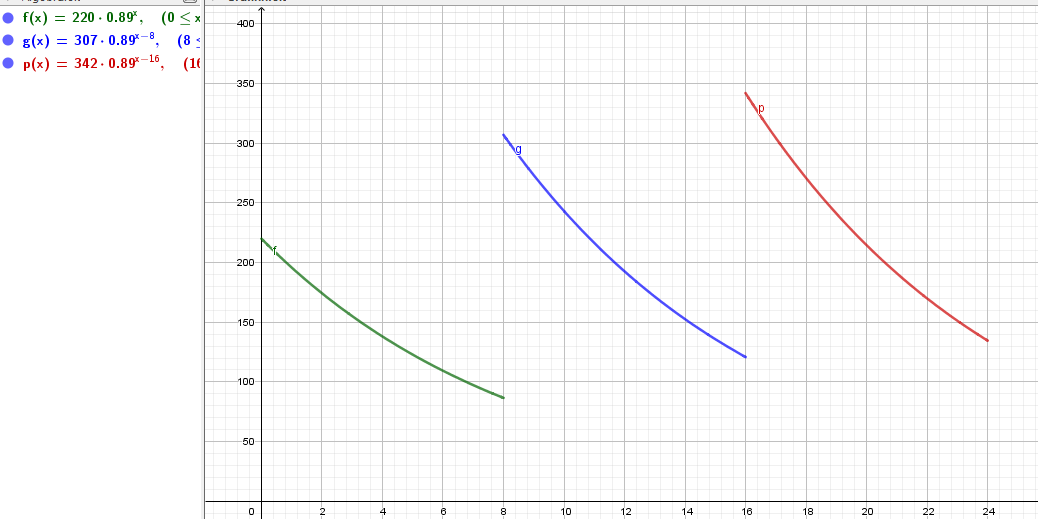
- Skjermbilde8.PNG (44.53 KiB) Viewed 1372 times
bilde 2
Det er dette jeg rett og slett ikke forstår omfanget av
Hvorfor gjør det å opphøye på denne måten slik at man "starter på nytt" på den gitte x-verdien (bilde 2) i stedet for å fortsette nedover slik som i bilde 1 over her?