Page 1 of 1
Trigonometriske likninger
Posted: 16/06-2019 12:46
by UnicornSpaceship
Hei, jeg skulle løse denne likninga og jeg henger med helt ned til de nederste trinnene, det jeg har markert. Det ser nesten ut som at den nederste generelle løsningen dekker over begge de to andre, men hvordan kan man komme frem til denne siste generelle løsningen, fra de andre?
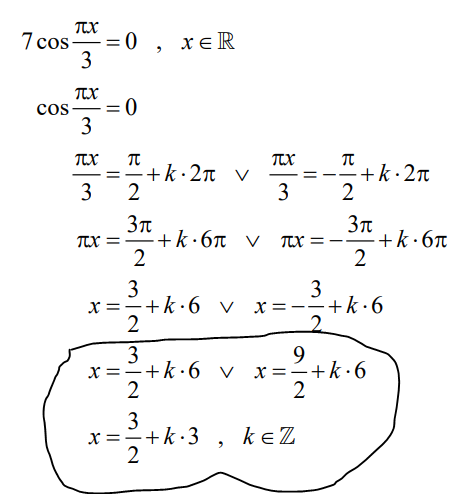
- Trigonometriske grunnlikninger.PNG (32.65 KiB) Viewed 2309 times
Re: Trigonometriske likninger
Posted: 16/06-2019 12:59
by Gustav
$x=\frac32+6k\, \vee x=\frac92+6k$
$x=\frac32+3(2k)\, \vee x=\frac32+3(2k+1)$.
som er det samme som å skrive
$x=\frac32+3n$, der uttrykket til venstre nest øverst dekker alle partallige n, og det til høyre dekker for alle odde n.
Re: Trigonometriske likninger
Posted: 16/06-2019 13:19
by UnicornSpaceship
Tusen takk for hjelpen! Jeg har faktisk et spørsmål til. Hvordan har det seg at man kan omfirme uttrykket slik?
[tex]x=-3/2+k*6 \rightarrow x=9/2+k*6[/tex]
Re: Trigonometriske likninger
Posted: 16/06-2019 14:00
by Aleks855
UnicornSpaceship wrote:Tusen takk for hjelpen! Jeg har faktisk et spørsmål til. Hvordan har det seg at man kan omfirme uttrykket slik?
[tex]x=-3/2+k*6 \rightarrow x=9/2+k*6[/tex]
-3/2 og 9/2 er det samme uttrykket, men med forskjellige $k$-verdier.