Page 1 of 1
geometry
Posted: 13/08-2019 16:43
by Janhaa
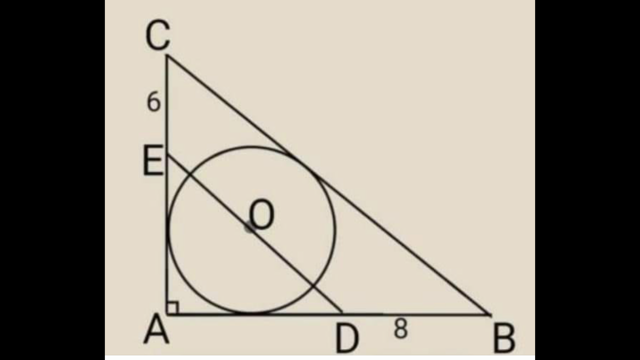
- math-trapezoid2.PNG (252.39 KiB) Viewed 11713 times
Finn omkretsen av trapeset BCED
Re: geometry
Posted: 13/08-2019 17:12
by Mattebruker
Finn først radius( r ) i sirkelen.
Elementær trekantrekning gir r = 2.
Finn deretter høgda på hypotenusen i dei to trekantane:
Største treakant: H = 4.8
Minste trekant: h = (4.8 - 2 ) = 2.8
Det lineare høvetalet [tex]\eta[/tex] = [tex]\frac{2.8}{4.8}[/tex] = [tex]\frac{7}{12}[/tex]
Resten av løysinga er rein plankekøyring.
Re: geometry
Posted: 13/08-2019 17:27
by Mattebruker
Omkrets = 10 + 10[tex]\cdot \frac{7}{12}[/tex] + (6 + 8 ) [tex]\cdot[/tex]( 1 - [tex]\frac{7}{12}[/tex] ) = [tex]\frac{65}{3}[/tex]
Re: geometry
Posted: 13/08-2019 17:54
by Guest
hvordan får du radien?
Re: geometry
Posted: 13/08-2019 18:12
by Mattebruker
Hvordan finner du radien r ?
Frå sentrum ( S ) i sirkelen trekkjer vi rette linestykke til hjørna i den store sirkelen. Da ser vi at
trekanten delast opp i tre mindre trekantar med felles toppunkt S. Høgda ( h ) frå S ned på sidene er lik r ( h = r ).
Da kan vi lett finne r ved å stille opp to uttrykk for arealet av den store trekanten.
Re: geometry
Posted: 13/08-2019 18:21
by Guest
må man anta at ad er lik ae
Re: geometry
Posted: 13/08-2019 19:33
by Mattebruker
svaret er nei !
Derimot er dei to trekantane( ABC og ADE ) likeforma !
Re: geometry
Posted: 14/08-2019 12:33
by Janhaa
Slenger inn to fasit-bidrag fra ulike kilder, begge gir omkrets 52.
bidrag 1:
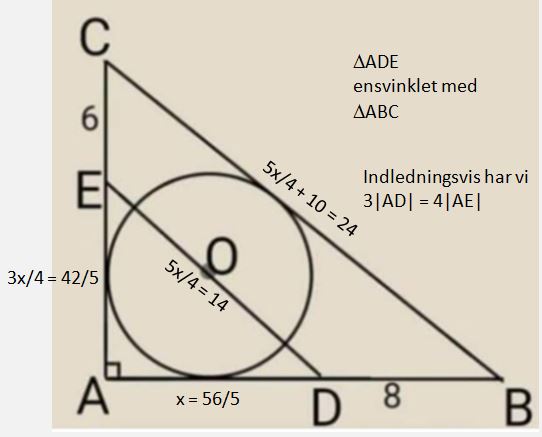
- trapezoid.jpg (30.61 KiB) Viewed 11630 times
Re: geometry
Posted: 14/08-2019 12:35
by Janhaa
Slenger inn to fasit-bidrag fra ulike kilder, begge gir omkrets 52.
bidrag 2:
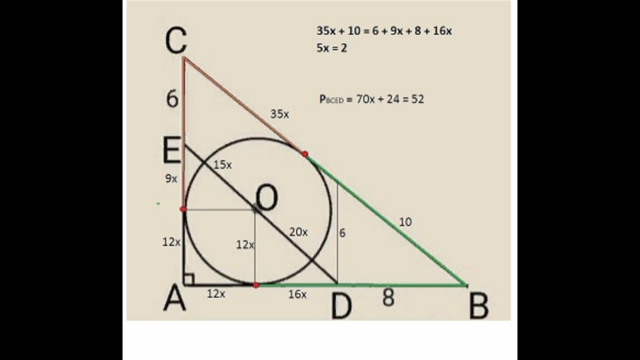
- solution-trapezoid.PNG (346.93 KiB) Viewed 11629 times
Re: geometry
Posted: 14/08-2019 17:26
by Mattebruker
Tok litt for lett på dette problemet. Høgda frå A ned på BC treffer ikkje tangeringspunktet for sirkelen med mindre trekanten er symmetrisk ( AB = AC ).