Page 1 of 1
Statistikk- median og gjennomsnitt
Posted: 08/01-2020 12:36
by aandersmm
Hei, jeg har forsøkt etter beste evne å løse oppgave 5.23 i Sigma Påbygging P. s 169
Ut ifra fasit klarte jeg oppgave a og d- såfremt noen halve poeng på de andre eller dels riktig.
Det jeg trenger hjelp til her er om jeg har gjort riktig i min fremstilling av oppgave b, hvorfor mitt svar i oppgave c er mindre riktig.
Og er besvarelsen min av oppgave e tilstrekkelig.
Er det noe jeg kunne gjort bedre tar jeg imot all hjelp.
Takker på forhånd.
mvh
Anders

- oppgaveteksten
- IMG_3381.JPG (2 MiB) Viewed 3359 times
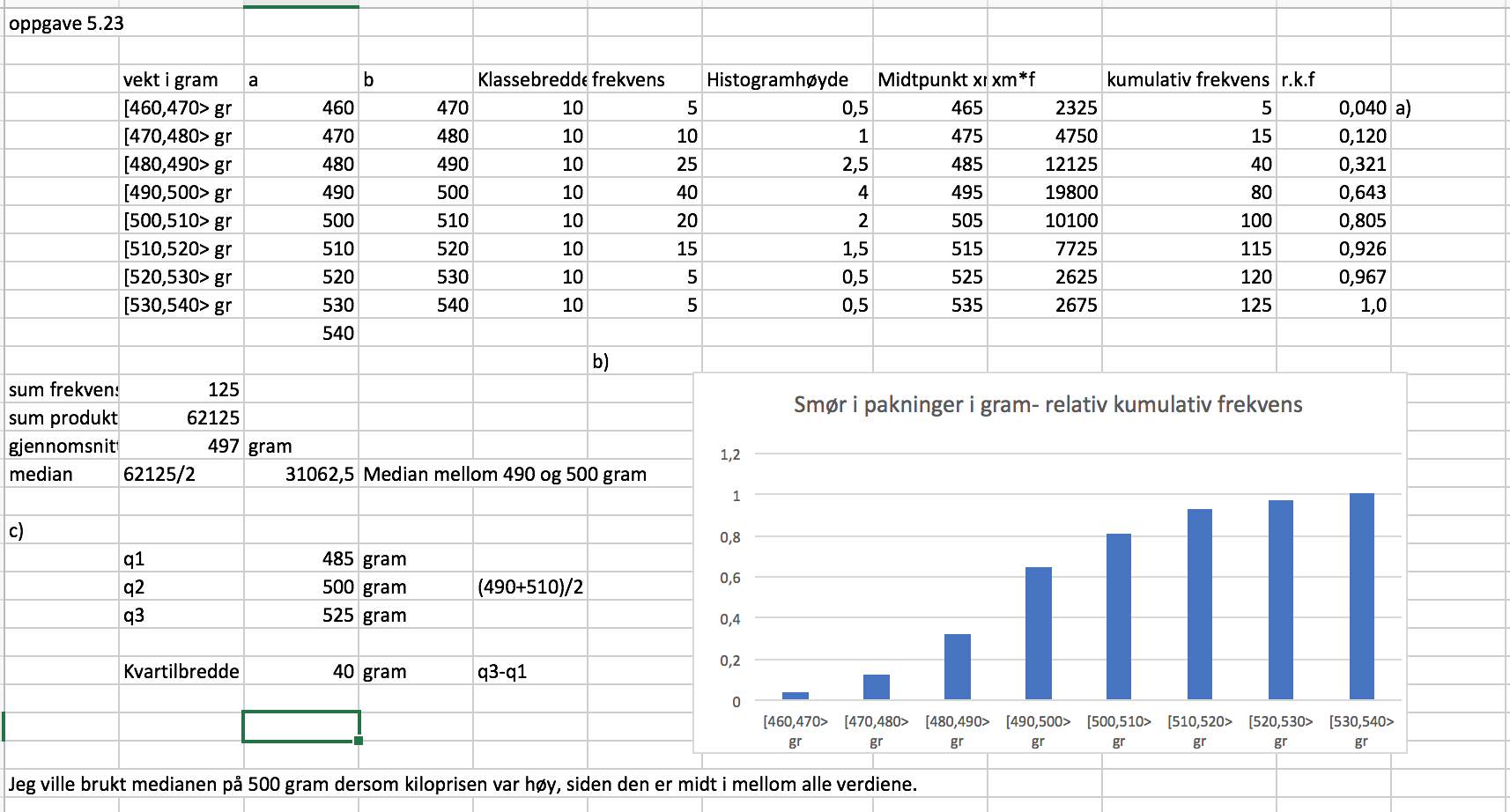
- oppgaven regnet ut i excel
- smør.png (186.16 KiB) Viewed 3359 times
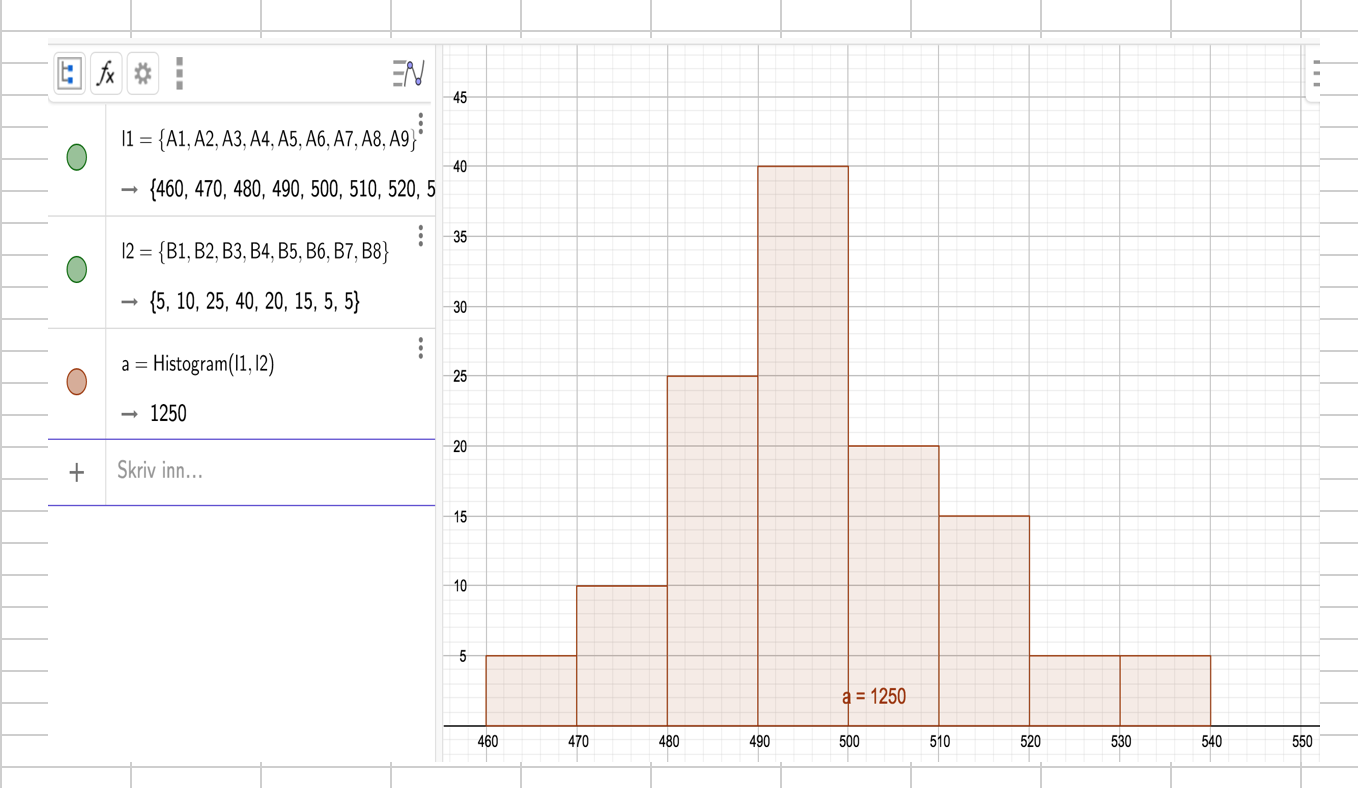
- histogram i geogebra
- Skjermbilde 2020-01-08 kl. 12.23.42.png (196.84 KiB) Viewed 3359 times
Re: Statistikk- median og gjennomsnitt
Posted: 08/01-2020 15:05
by Kristian Saug
Hei Anders,
I denne oppgaven bør man bruke linjediagram for å illustrere den relative kumulative frekvensen på best måte.
Dermed kan man lese av grafisk hva median og nedre/øvre kvartil er.
Det lar seg ikke gjøre ut i fra et søylediagram.
Se vedlegg med komplett besvarelse.
Re: Statistikk- median og gjennomsnitt
Posted: 09/01-2020 11:42
by aandersmm
Kristian Saug wrote:Hei Anders,
I denne oppgaven bør man bruke linjediagram for å illustrere den relative kumulative frekvensen på best måte.
Dermed kan man lese av grafisk hva median og nedre/øvre kvartil er.
Det lar seg ikke gjøre ut i fra et søylediagram.
Se vedlegg med komplett besvarelse.
Tusen takk for svar.
i oppg a- brukte jeg tallmaterialet som er oppgitt og ikke histogramhøyden som jeg regnet ut. Får jeg ikke full uttellling da, selv om de ser like ut?
Se vedlegg for spesifikke spørsmål til oppgaven som jeg ikke forstår.
La inn zip fil da word dokumentet mitt ble for stort.
Si ifra om den ikke kan åpnes.
mvh
Anders
Re: Statistikk- median og gjennomsnitt
Posted: 09/01-2020 12:31
by Kristian Saug
Hei igjen, Anders
I et histogram må du ha med høyden på søylene. Poenget er at intervallbredde * høyde = frekvens. Slik skal man lese ut av et histogram!
I linjediagrammet ditt har det sneket seg inn en slurvefeil. Ditt viser t.o.m 530 gram, men det skal vise t.o.m 540 gram. Dermed har du fått feil verdier på skjæringspunkt.
Se over tabellen du har brukt, så finner du nok feilen!
Re: Statistikk- median og gjennomsnitt
Posted: 09/01-2020 16:25
by aandersmm
Kristian Saug wrote:Hei igjen, Anders
I et histogram må du ha med høyden på søylene. Poenget er at intervallbredde * høyde = frekvens. Slik skal man lese ut av et histogram!
I linjediagrammet ditt har det sneket seg inn en slurvefeil. Ditt viser t.o.m 530 gram, men det skal vise t.o.m 540 gram. Dermed har du fått feil verdier på skjæringspunkt.
Se over tabellen du har brukt, så finner du nok feilen!
Da fikk den jeg til å gå opp og forsto mer av det, takk.
mvh
Anders
Re: Statistikk- median og gjennomsnitt
Posted: 09/01-2020 16:44
by aandersmm

- IMG_3384.jpg (2.07 MiB) Viewed 3293 times

- fasit
- IMG_3385.jpg (1.94 MiB) Viewed 3293 times
Hei igjen, her kommer en ny oppgave som jeg har forsøkt å løse i dag.
5.24 samme bok, samme side.
Problemet mitt her som jeg har skrevet i vedlegget som er ett word dokument er at jeg ikke får til annet enn typetall og gjennomsnittet i oppgaven.
Bommer svært mye, og klarer ikke helt å se hva jeg gjør feil.
Takker for all hjelp på forhånd
mvh
Anders
Re: Statistikk- median og gjennomsnitt
Posted: 09/01-2020 18:36
by Kristian Saug
Hei,
For å hjelpe deg best, gjorde jeg hele oppgaven.
Se vedlegg for løsningsforslag med forklaringer.
Re: Statistikk- median og gjennomsnitt
Posted: 10/01-2020 11:00
by aandersmm
Takk for svar.
Utover oppgaven har jeg vært forvirret om hvor det gjelder mål og hvor det gjelder kamper (er det en enkel måte og kunne forstå dette). Men fra det vi skal finne ut skal det jo være mål siden det er det oppgaven spør etter.
Jeg ser at jeg hadde feil på antall mål per kamp 6 som skulle være 11, jeg hadde skrevet 1. Der var første feil som ordnet opp en del, da fikk jeg riktig gjennomsnitt blant annet.
Median faller inn under partall, og da er det n/2 +n/2+1 - som er 66/2+(66/2)+1= 66,5. Siden vi tar ut ifra kumulative frekvensen, jeg ble forvirret da du tok det fra x-antall mål i stedet for.
"Hvis det er n obervasjoner i datamaterialet, er median gitt ved (regelen som jeg skrev ovenfor)"
Hva er riktig?
mvh
Anders
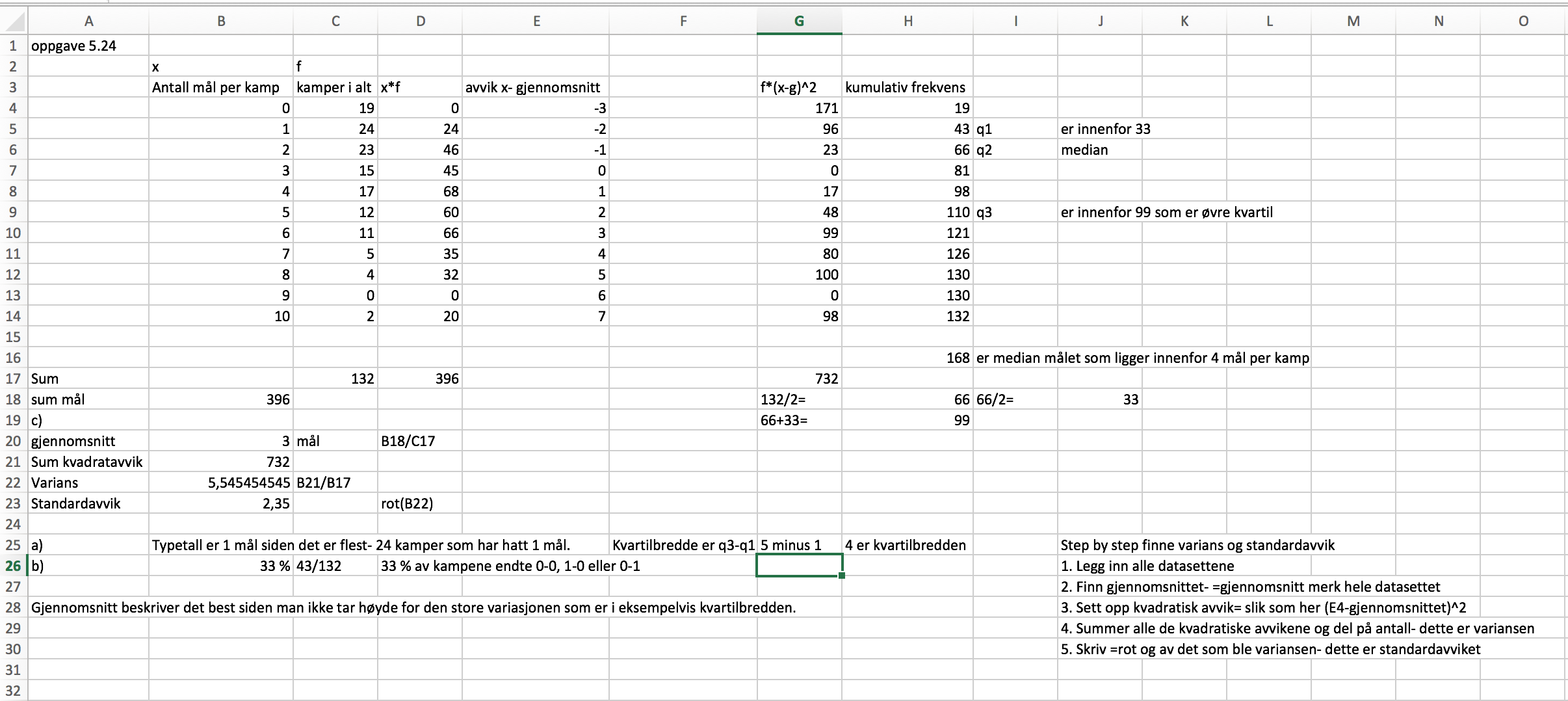
- Endringer på besvarelsen min
- Skjermbilde 2020-01-10 kl. 10.56.06.png (306.24 KiB) Viewed 3258 times
Re: Statistikk- median og gjennomsnitt
Posted: 10/01-2020 22:09
by Kristian Saug
Hei,
Beklager sent svar. Jeg så ditt siste innlegg nå.
Observasjonene er sortert i stigende rekkefølge, fra 0 mål til 10 mål. Det er gjort 132 observasjoner.
Median er den midterste observasjonen. Det blir i dette tilfellet observasjon nr 66 (2 mål) og nr 67 (3 mål).
Medianen blir således [tex]\frac{(2 + 3)}{2}[/tex] mål = 2,5 mål.
Samme prinsipp gjelder for nedre og øvre kvartil, som tidligere forklart i løsningsforslaget.
Re: Statistikk- median og gjennomsnitt
Posted: 13/01-2020 11:31
by aandersmm
Kristian Saug wrote:Hei,
Beklager sent svar. Jeg så ditt siste innlegg nå.
Observasjonene er sortert i stigende rekkefølge, fra 0 mål til 10 mål. Det er gjort 132 observasjoner.
Median er den midterste observasjonen. Det blir i dette tilfellet observasjon nr 66 (2 mål) og nr 67 (3 mål).
Medianen blir således [tex]\frac{(2 + 3)}{2}[/tex] mål = 2,5 mål.
Samme prinsipp gjelder for nedre og øvre kvartil, som tidligere forklart i løsningsforslaget.
OK, det gir litt mer mening og tenke alt som observasjoner da det handler om mål her.
"Median faller inn under partall, og da er det n/2 +n/2+1"- det er derfor du snakker om mål 66 og 67?
mvh
Anders
Re: Statistikk- median og gjennomsnitt
Posted: 13/01-2020 11:53
by Kristian Saug
aandersmm wrote:Kristian Saug wrote:Hei,
Beklager sent svar. Jeg så ditt siste innlegg nå.
Observasjonene er sortert i stigende rekkefølge, fra 0 mål til 10 mål. Det er gjort 132 observasjoner.
Median er den midterste observasjonen. Det blir i dette tilfellet observasjon nr 66 (2 mål) og nr 67 (3 mål).
Medianen blir således [tex]\frac{(2 + 3)}{2}[/tex] mål = 2,5 mål.
Samme prinsipp gjelder for nedre og øvre kvartil, som tidligere forklart i løsningsforslaget.
OK, det gir litt mer mening og tenke alt som observasjoner da det handler om mål her.
"Median faller inn under partall, og da er det n/2 +n/2+1"- det er derfor du snakker om mål 66 og 67?
mvh
Anders
Det er 132
observasjoner i denne oppgaven, der hver observasjon er en fotballkamp. Tenk deg at du observerer antall mål i hver kamp. Deretter
sorteres kampene (observasjonene)
etter antall mål som er scoret. Kampene med 0 mål stilles først i rekken, deretter kampene med 1 mål osv. Da ser vi at observasjon nr 66 har 2 mål og observasjon nr 67 har 3 mål. Dette er de
to midterste observasjonene og utgjør dermed
medianen som blir gjennomsnittet av antall mål i disse to kampene,
2,5 mål. For all del, det ble
ikke scoret 66 eller 67 mål i noen av kampene.
Jeg anbefaler deg å gjøre noen oppgaver til av samme slag. Så kan du stille evt spørsmål til læreren og/eller her på forumet. Viktig at dette sitter, for det er høyaktuelt på en eksamen!