Page 1 of 1
dag 18
Posted: 18/12-2020 12:07
by Janhaa
- trekant-kvadrat.png (6.74 KiB) Viewed 25399 times
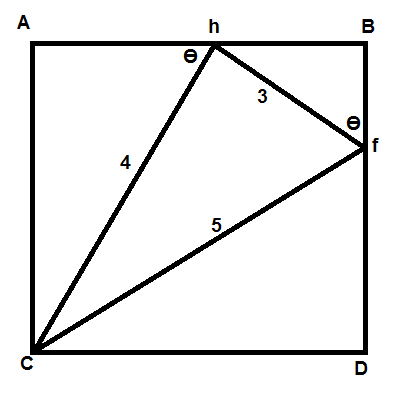
En trekant er innskrevet i et kvadrat. Finn arealet til kvadratet?
Re: dag 18
Posted: 18/12-2020 13:25
by Mattebruker
Areal ( kvadrat ) = [tex]\frac{256}{17}[/tex]
Re: dag 18
Posted: 18/12-2020 13:47
by Guest
gitt at firkanten ikke er en saccheri eller lambert firkant:
[tex]\left \{ a^2+(a-b)^2=25,a^2+(a-x)^2=16,b^2+x^2=9 \right \}[/tex]
[tex]\left \{x=\frac{12}{17}\sqrt{17},a=\frac{16}{17}\sqrt{17},b=\frac{3}{17}\sqrt{17} \right \}[/tex]
[tex]a^2=(\frac{16}{17}\sqrt{17})^2[/tex]
Re: dag 18
Posted: 20/12-2020 15:32
by Janhaa
Gjest wrote:gitt at firkanten ikke er en saccheri eller lambert firkant:
[tex]\left \{ a^2+(a-b)^2=25,a^2+(a-x)^2=16,b^2+x^2=9 \right \}[/tex]
[tex]\left \{x=\frac{12}{17}\sqrt{17},a=\frac{16}{17}\sqrt{17},b=\frac{3}{17}\sqrt{17} \right \}[/tex]
[tex]a^2=(\frac{16}{17}\sqrt{17})^2[/tex]
sjølsagt korrekt.