Page 1 of 1
Vektorer
Posted: 20/04-2021 18:13
by themol1
Hei!
Noen som kan forklare meg forskjellen på de to uttrykkene som ligger vedlagt i .png-fila?
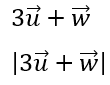
- Skjermbilde.PNG (1.49 KiB) Viewed 3169 times
På forhånd takk

Re: Vektorer
Posted: 20/04-2021 18:29
by Mattebruker
|3[tex]\overrightarrow{u}[/tex] + [tex]\overrightarrow{w}[/tex]| er lengda ( skalarverdien - pos. reelt tal ) av vektoren 3[tex]\overrightarrow{u}[/tex] + [tex]\overrightarrow{w}[/tex].
|3[tex]\overrightarrow{u}[/tex] + [tex]\overrightarrow{w}[/tex]| = ( pr. def. ) [tex]\sqrt{(3\overrightarrow{u}+ \overrightarrow{w})^{2}}[/tex]
Re: Vektorer
Posted: 20/04-2021 18:39
by themol1
Mattebruker wrote:|3[tex]\overrightarrow{u}[/tex] + [tex]\overrightarrow{w}[/tex]| er lengda ( skalarverdien - pos. reelt tal ) av vektoren 3[tex]\overrightarrow{u}[/tex] + [tex]\overrightarrow{w}[/tex].
|3[tex]\overrightarrow{u}[/tex] + [tex]\overrightarrow{w}[/tex]| = ( pr. def. ) [tex]\sqrt{(3\overrightarrow{u}+ \overrightarrow{w})^{2}}[/tex]
[tex]u=[3,1] w=[-6,-2][/tex]
Dersom u og w har disse verdiene, hva vil da svaret på nr. 2 bli? Altså oppgaven nederst i bildet ...
Den øverste har jeg funnet svaret på: 3, 1
Re: Vektorer
Posted: 20/04-2021 18:42
by SveinR
Hei, for å finne lengden av $3\vec{u} + \vec{w}$ er det en fordel å først regne ut denne vektoren.
Da får vi $3\vec{u} + \vec{w} = 3\cdot [3, 1] + [-6, -2] = [9, 3] + [-6, -2] = [3, 1]$
Lengden av en vektor kan vi deretter finne fra Pytagoras - vektoren danner en rettvinklet trekant med $x$-koordinaten som lengden av den ene kateten og $y$-koordinaten som lengden av den andre kateten. Lengden av vektoren blir dermed tilsvarende lengden av hypotenusen.
Re: Vektorer
Posted: 20/04-2021 19:06
by themol1
SveinR wrote:Hei, for å finne lengden av $3\vec{u} + \vec{w}$ er det en fordel å først regne ut denne vektoren.
Da får vi $3\vec{u} + \vec{w} = 3\cdot [3, 1] + [-6, -2] = [9, 3] + [-6, -2] = [3, 1]$
Lengden av en vektor kan vi deretter finne fra Pytagoras - vektoren danner en rettvinklet trekant med $x$-koordinaten som lengden av den ene kateten og $y$-koordinaten som lengden av den andre kateten. Lengden av vektoren blir dermed tilsvarende lengden av hypotenusen.
Vil det da si at svaret er: [tex]=|3\vec u+\vec w|=\sqrt{3^2+1^2}=\sqrt{10}[/tex]
Re: Vektorer
Posted: 20/04-2021 19:30
by SveinR
Jepp, det stemmer

Re: Vektorer
Posted: 21/04-2021 00:55
by themol1
Er det noen forskjell på disse to oppgavene? eller vil svarer være likt i begge to?
Dersom det trengs:
u = [3, 1]
v = [-8,4]
w = [-6,-2]
Re: Vektorer
Posted: 21/04-2021 12:37
by LektorNilsen
themol1 wrote:Er det noen forskjell på disse to oppgavene? eller vil svarer være likt i begge to?
Dersom det trengs:
u = [3, 1]
v = [-8,4]
w = [-6,-2]
Det blir ikke samme svar.
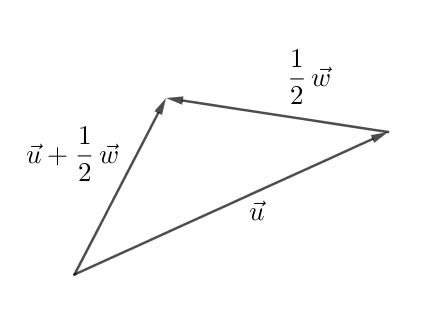
Tenk deg at vektor u var en vektor mellom Kristiansand og Oslo og at vektor w var en vektor mellom Oslo og Bergen.
Da vil det øverste uttrykket beskrive avstanden i luftlinje fra Kristiansand til et punkt halvveis mellom Oslo og Bergen, mens uttrykket under vil være summen av avstanden i luftlinje mellom Kristiansand og Oslo og halve avstanden i luftlinje mellom Oslo og Bergen.
Se vedlagt illustrasjon:
- Skjermbilde 2021-04-21 kl. 12.42.19.png (19.81 KiB) Viewed 3108 times
