Page 1 of 1
polynomdivisjon for å finne skrå asymptote
Posted: 08/10-2022 13:58
by LeHas
Kan noen hjelpe meg med å løse dette regnestykket ved hjelp av polynomdivisjon? Jeg har prøvd men får det ikke til. Takk på forhånd
2x^2 + 3x - 4 : 2x - 4
Re: polynomdivisjon for å finne skrå asymptote
Posted: 08/10-2022 15:21
by SveinR
Hva har du kommet frem til? Hvor stopper det?
Re: polynomdivisjon for å finne skrå asymptote
Posted: 08/10-2022 15:42
by LeHas
2x^2 + 3x - 4 : 2x - 4 = x
- (2x^2 - 4x)
7x - 4
Kommer ikke lenger enn dette
Re: polynomdivisjon for å finne skrå asymptote
Posted: 08/10-2022 22:25
by SveinR
Du er på god vei!
Det neste vi da må tenke er: "Hvordan kan vi få $2x$ til å bli $7x$?"
Og det vi må gange $2x$ med da, er $\frac{7}{2}$. Kommer du videre nå?
Re: polynomdivisjon for å finne skrå asymptote
Posted: 08/10-2022 23:06
by LeHas
Jeg kommer videre ja men nå sitter jeg fast igjen. Jeg sliter litt med å finne ut hva jeg skal gange med hva for å komme videre. Nå har jeg dette som svar, med 10 i rest.
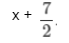
- 722.PNG (1.03 KiB) Viewed 6129 times
Re: polynomdivisjon for å finne skrå asymptote
Posted: 08/10-2022 23:29
by SveinR
Da er du nesten der! Resten på $10$ betyr at du da ender opp med, som resultatet av polynomdivisjonen:
$x + \frac{7}{2} + \frac{10}{2x-4}$
Og det betyr igjen at det opprinnelige brøkuttrykket ditt kan skrives om til dette:
$\frac{2x^2+3x-4}{2x-4}=x + \frac{7}{2} + \frac{10}{2x-4}$
Hva kan dette da fortelle deg om den skrå asymptoten til uttrykket? Hva skjer med uttrykket til høyre når $\lim_{x\rightarrow\pm\infty}$?
Re: polynomdivisjon for å finne skrå asymptote
Posted: 09/10-2022 11:53
by LeHas
Det blir tilnærmet lik 0? Som betyr at funksjonen vil gå mot x, så den skrå asymptoten blir y = x
Re: polynomdivisjon for å finne skrå asymptote
Posted: 09/10-2022 12:58
by SveinR
Det siste leddet vil gå mot $0$ ja, og da står vi igjen med $x+\frac{7}{2}$ som den skrå asymptoten. Tegner du grafene til $\frac{2x^2+3x-4}{2x-4}$ og til $x+\frac{7}{2}$, vil du se at dette stemmer

Re: polynomdivisjon for å finne skrå asymptote
Posted: 09/10-2022 14:13
by LeHas
Skjønner! Tusen takk for hjelpen:)