Page 1 of 1
Omskriving av formel
Posted: 24/10-2022 15:53
by LeHas
Hvordan får jeg
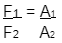
- F1.PNG (659 Bytes) Viewed 3828 times
Til å bli
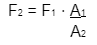
- f2.PNG (691 Bytes) Viewed 3828 times
Re: Omskriving av formel
Posted: 24/10-2022 16:57
by SveinR
$\frac{F_1}{F_2} = \frac{A_1}{A_2}$
En litt omstendelig metode først:
Vi ønsker å løse for $F_2$, så vi må få den vekk fra å være under brøkstreken. Da kan vi gange begge sider av likningen med $F_2$:
$\frac{F_1}{F_2}\cdot \textcolor{red}{F_2} = \frac{A_1}{A_2}\cdot\textcolor{red}{F_2}$
Det gir:
$F_1 = \frac{A_1\cdot F_2}{A_2}$
Siden vi ønsker å få $F_2$ alene, kan vi nå gange begge sider med $A_2$ for å bli kvitt denne brøken:
$F_1 \cdot \textcolor{red}{A_2}= \frac{A_1\cdot F_2}{A_2}\cdot \textcolor{red}{A_2}$
Det gir:
$F_1\cdot A_2 = A_1\cdot F_2$
Det eneste som mangler nå for å få $F_2$ alene er å dele begge sider med $A_1$:
$\frac{F_1\cdot A_2}{\textcolor{red}{A_1}} = \frac{A_1\cdot F_2}{\textcolor{red}{A_1}}$
Det gir, helt til slutt:
$\frac{F_1\cdot A_2}{A_1} = F_2$
Dette er helt ekvivalent med å sette
$F_2 = F_1\cdot \frac{A_2}{A_1}$
Vi ser også at dette ikke er fasitsvaret ditt, som betyr at det er en feil i den fasiten.
Re: Omskriving av formel
Posted: 24/10-2022 17:00
by SveinR
En litt kjappere metode her:
Hvis $\frac{F_1}{F_2} = \frac{A_1}{A_2}$, så vet vi også at den omvendte sammenhengen gjelder:
$\frac{F_2}{F_1} = \frac{A_2}{A_1}$ (test gjerne med noen tall for å se at dette gjelder!)
Og da er vi nesten i mål allerede, det eneste vi trenger å gjøre er å gange opp med $F_1$:
$\frac{F_2}{F_1}\cdot\textcolor{red}{F_1} = \frac{A_2}{A_1}\cdot\textcolor{red}{F_1}$
Som igjen gir:
$F_2 = F_1\cdot\frac{A_2}{A_1}$