En nøtt
Posted: 23/04-2006 17:22
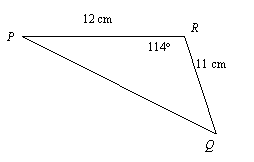
a) Finn lengden av PQ på figuren
b) Karl Fredrik jobber i et hagesenter. Han får en bestilling på jord til en trekantet hage ABC. Han får oppgitt følgende mål: Vinkel CAB = 44 grader,
AC = 9,0 m og BC = 7,0 m. Jordlaget skal være 10 cm dypt.
1. Forklar hvorfor Karl Fredrik trenger mer informasjon fra kunden.
2. Hva er det størst mulige volumet av jord som trengs hvis kunden ikke gir mer informasjon.
På forhånd takk

b) Karl Fredrik jobber i et hagesenter. Han får en bestilling på jord til en trekantet hage ABC. Han får oppgitt følgende mål: Vinkel CAB = 44 grader,
AC = 9,0 m og BC = 7,0 m. Jordlaget skal være 10 cm dypt.
1. Forklar hvorfor Karl Fredrik trenger mer informasjon fra kunden.
2. Hva er det størst mulige volumet av jord som trengs hvis kunden ikke gir mer informasjon.
På forhånd takk