1P 2012 vår LØSNING
DEL EN
Oppgave 1:
a)
Overslag:
$14,90 kr \approx 15 kr \\ 48,50 kr \approx 50 kr \\ 15kr \cdot 6 + 2,5 \cdot 50kr = 90 kr + 125kr = 215 kr$
Hun må betale i underkant av 215 kr.
b)
Trekant ABC er likesidet og har omkrets 3 +3 +3 = 9
Trekant DEF er rettvinklet. Lengden av DF er $DF = \sqrt{16-4} = \sqrt{12}$
Siden kvadratroten av tolv er større enn tre har trekanten DEF størst omkrets.
c)
Forskjellen delt på pris herreklipp ganger hundre:
$\frac{240kr}{400kr} \cdot 100 = 60%$
d)
Når noe minker med 15% per år blir vekstfaktoren 1-0,15 = 0,85.
Alternativ tre er derfor riktig.
e
I basisåret er KPI = 100. En vare som koster 100 kr i basisåret vil til enhver tid ha en verdi tilsvarende KPI, forutsatt at den har en prisutvikling som følger indeksen.
$kroneverdi = \frac{100}{kpi} \\ 0,8 = \frac {100}{KPI} \\ KPI = 125$
Varen vil koste kr. 125, i 2009.
f)
Dersom høyde og diameter er omvendt proporsjonal er høyde ganger diameter konstant. Konstanten er tjuefire ganger ti som er 240.
$\frac{240}{6} = 40 \\ \frac{240}{12}= 20$
Diameterne er henholdsvis 40cm. og 20cm.
g)
Sannsynligheten for å få seks øyner med en terning er en sjettedel (gunstige delt på mulige).
Med to terninger det seks ganger seks mulige utfall, altså 36. Det er seks av disse som vil gi to like. Sannsynligheten blir da seks delt på trettiseks, som også er en sjettedel.
Sannsynlighetene er de samme.
h)
Dersom man setter pi lik tre blir areal av det sorte området areal av sirkel minus areal av trekant:
$A= \pi r^2 - \frac {gh}{2} = 3 \cdot 4 \cdot 4 - \frac{8 \cdot 4}{2} = 48 -16 = 32$
Arealet av det sorte området er 32.
i)
1)
| Fotball | Ikke Fotball | TOTAL | |
|---|---|---|---|
| Håndball | 6 | 4 | 10 |
| Ikke Håndball | 9 | 1 | 10 |
| TOTAL | 15 | 5 | 20 |
2)
Sannsynligheten for at en elev spiller håndball, når vi vet eleven spiller fotball;
$P(H|F)= \frac{6}{15} = 40\percent$
Oppgave 2:
a)
Hele posen er 150 gram. 30 gram gir 150kcal. Han spiser hele posen som er 150 gram, 5 ganger mere enn 30 gram. Han får da i seg 5 ganger 150kcal, Dvs. 750 kcal.
b)
$E = (P+K) \cdot 4 + F \cdot 9 \\ 150 = (2 +K) \cdot 4 + 8 \cdot 9 \\ 150 = 8+ 4K + 72 \\4K= 70 \\ K= 17,5$
Det er 17,5 gram karbohydrater i 30 gram potetskiver.
Oppgave 3:
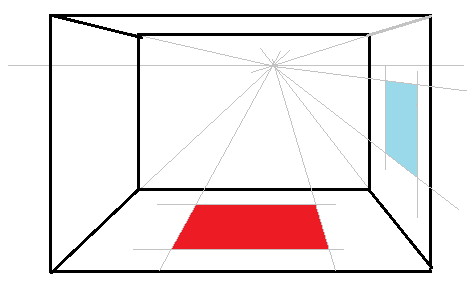
a og b)
Oppgave 4:
a)
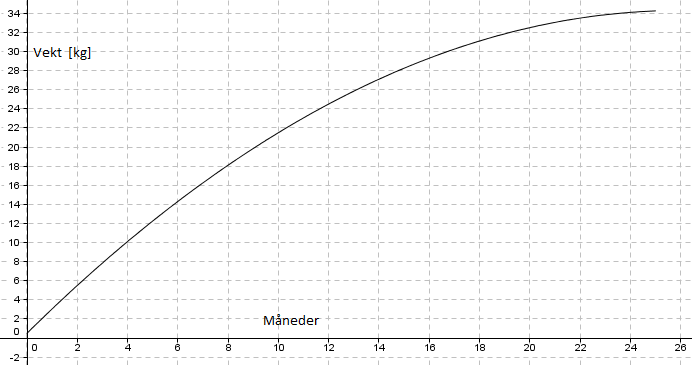
$f(x) = -0,05x^2+2,60x+0,50$
Når x er null er f lik 0,50, dvs. grisen veide 0,50 kg ved fødselen.
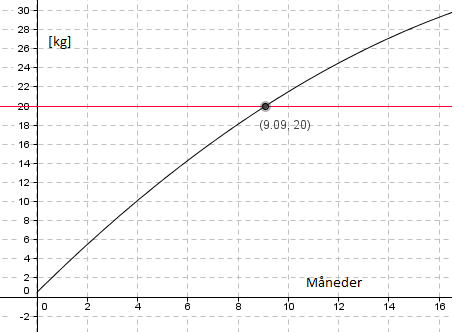
b)
Grisen vil passere 20 kg etter ca. 9 måneder.
Gjennomsnittlig vektøkning per måned:
$\frac{19,5kg}{9,1mnd} = 2,1kg/mnd$
Oppgave 5:
a)
To rosa:
$\frac{2}{10} \cdot \frac 19 = \frac{1}{45}= 0,022$
b)
Hun kan trekke rosa i første eller andre trekket:
P(kun en rosa på to trekk) = $ \frac{2}{10} \cdot \frac{8}{9} +\frac{8}{10} \cdot \frac{2}{9} = 0,355 $
c)
Det er fem forskjellige farger. Man multipliserer sannsynligheten i a) med fem og får:
$0,022 \cdot 5 = 0,11$
Det er ca. 11% sannsynlig at hun trekker to like sokker.
Oppgave 6:
a)
$2300 = 10a+b \\ 3200 = 16a + b \\ ---\\ 2300 = 10a + (3200 - 16a) \\ a = 150 \wedge b = 800$
b)
a, "stigningstallet" er prisen for er lass sand. b er prisen for kjøring, altså konstantleddet.
Oppgave 7:
a)
Gammel dusj: 10 l :35 s= 0,2857 l/s Ny dusj: 10 l : 65 s = 0,1538 l/s
Vannførbruk gammel dusj: $ 60s \cdot 8 \cdot 0,2857 l/s = 137,1 l$
Vannforbruk ny dusj: $60 s \cdot 8 \cdot 0,1538 l/s = 73,8 l$
b)
Kostnader ved gammel dusj per år: $0,035kWh/l \cdot 1,10 kr/kWh \cdot 365 \cdot 137,1 l = 1927kr/år $
c)
Vannmengde spart per dag:137-74 = 63 liter.
Daglige kostnader spart: $63 \cdot 0,0385 = 2,43$ kr
$\frac{400kroner}{2,43 kroner/dag} = 165$ dager
d)
$V= l \cdot b \cdot h = 14dm \cdot 5 dm \cdot 3 dm = 201 liter \\ 210 \cdot 0,0385 = 8,09$
Det koster ca 8 kroner å fylle badekaret med varmt vann.
Oppgave 8:
a)
Leser fra grafene:
Blokkleilighet ca. 6 år.
Småhus ca 7,5 år.
Eneboliger ca, 9 år.
b)
Indeksen har økt fra ca. 100 til 225 i perioden.
$2,25 \cdot 1,35 mil = 3,0 mil$
Eneboligen har en verdi på ca. 3 mil i begynnelsen av 2004.
c)
$\frac{150}{100} = \frac {100}{x} \\ x =67$ Da ville indeksen vært 67.
d)
Fra figuren ser man at leiligheter steg fra ca. 100, til ca. 300, en økning på 200%. Den samme økningen for eneboliger var på ca. 100%. så, ja, det er riktig når man tar utgangspunkt i prosentvis økning.
Oppgave 9:
a)
Bruker Pytagoras: $h = \sqrt{17^2-5^2} = 16,25$
Høyden i de likebeinte trekantene er 16,25cm. Overflaten av pyramiden blir da:
$A = 4 \cdot \frac{g \cdot h}{2} +k^2 = \\ 4 \cdot \frac{10cm \cdot 16,25cm}{2} + (10cm)^2 = 424 cm^2$
Arealet av pyramidekortet er ca. 424 kvadratsentimeter.
b)
Bruker Pytagoras nok en gang:
$h = \sqrt{16,25^2-5^2} = 15,5$
Høyden er ca. 15,5 cm.
c)
10 cm. over grunnflaten er 5,5 cm. under toppen. Bruker formlike trekanter og får:
$ \frac{15,5}{5,5} = \frac{10}{x} \\ x = 3,6 $
Hullet må være kvadratisk med sider ca, 3,6 cm. lange.