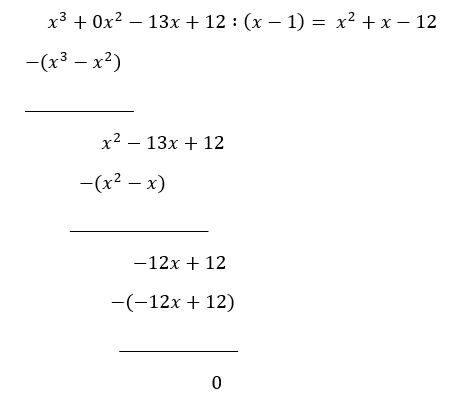R1 2018 vår LØSNING
Diskusjon av denne oppgaven på matteprat
Løsningsforslag (pdf) (open source, meld fra om forbedringer eller feil her)
Løsningsforslag av LektorNilsen (pdf)
Løsning som video av Lektor Håkon Raustøl
DEL 1
Oppgave 1
a)
$f(x)=x^4-x+2$
$f'(x)=4x^3-1$
b)
$g(x)=x^3\cdot ln(x)$
$g'(x)=3x^2\cdot ln(x) + x^3 \cdot \frac{1}{x} = 3x^2ln(x)+x^2$
c)
$h(x)=e^{2x^2+x}$
$h'(x)=(4x+1)e^{2x^2+x}$
Oppgave 2
a)
$\frac{1}{2x-2}+\frac{2}{x-3}-\frac{x-2}{x^2-4x+3} \\ = \frac{1\cdot \color{blue}{(x-3)}}{2(x-1)\color{blue}{(x-3)}}+\frac{2\cdot \color{red}{2(x-1)}}{\color{red}{2(x-1)}(x-3)}-\frac{\color{orange}{2}(x-2)}{\color{orange}{2}(x-1)(x-3)} \\ =\frac{ (x-3) + (4x-4) - (2x-4)}{2(x-1)(x-3)} \\ = \frac{x+4x-2x -3-4+4}{2(x-1)(x-3)} \\ = \frac{3x-3}{2(x-1)(x-3)} \\ = \frac{3(x-1)}{2(x-1)(x-3)} \\ = \frac{3}{2(x-3)} \\ = \frac{3}{2x-6}$
b)
$2ln(x\cdot y^3)-\frac{1}{2}ln(\frac{x^4}{y^2}) \\ = 2(ln(x)+ln(y^3))-\frac{1}{2}(ln(x^4)-ln(y^2)) \\= 2(ln(x)+3ln(y))-\frac{1}{2}(4ln(x)-2ln(y)) \\= 2ln(x)+6ln(y)-2ln(x)+ln(y) \\= 7ln(y)$
Oppgave 3
Vi har punktene A(-2,-1), B(-1, -3), C(3, -1) og D(t,t^2+2) der $t\in R$.
a)
$\vec{AB} = [-1-(-2), -3-(-1)] = [1, -2]$
$\vec{BC} = [3-(-1), -1-(-3)] = [4, 2]$
b)
$[1,-2]\cdot[4,2] = 1\cdot 4 + (-2)\cdot 2 = 4-4 = 0$
Skalarproduktet av $\vec{AB}$ og $\vec{BC}$ er 0, og vi har derfor $\vec{AB}\perp\vec{BC}$
c)
$\vec{CD}=[t-3, t^2+2-(-1)] = [t-3, t^2+3]$
Dersom $\vec{CD}\| \vec{AB}$, så er $\vec{CD} = k\cdot\vec{AB}$
$[t-3,t^2+3]=k\cdot[1,-2]$
Vi får likningssettet:
$I \quad t-3 = k$
$II \quad t^2+3=-2k$
$II \quad t^2+3 = -2 (t-3) \\ \quad t^2 + 3 = -2t+6 \\ \quad t^2 + 2t -3 = 0 \\ \quad (t+3)(t-1) = 0 \\ \quad t = -3 \vee t = 1$
$\vec{CD}\| \vec{AB}$ når $ t = -3 \vee t = 1$.
Oppgave 4
Vi har $f(x)=x^3+k\cdot x + 12$
a)
Dersom $f(x):(x-1)$ skal gå opp, er x=1 et nullpunkt.
$f(1)=0 \\ 1^3+k\cdot 1 + 12 = 0 \\ k+13 = 0 \\ k=-13$
b)
Vi har nå $f(x)=x^3-13x+12$
Utfører polynomdivisjonen:
$f(x)=(x^2+x-12)(x-1) = (x-3)(x-1)(x+4)$
c)
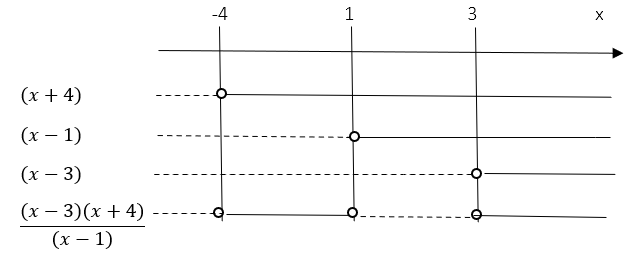
$\frac{x^2+x-12}{x-1} \geq 0 \\ \frac{(x-3)(x+4)}{x-1} \geq 0$
$\frac{x^2+x-12}{x-1} \geq 0$ nå $x\in [-4,1]\cup [3,\rightarrow \rangle$
Oppgave 5
D = defekt
a)
$P(A \cap D) = 0,40 \cdot 0,03 = 0,012 = 1,2 \%$
Sannsynligheten for at laderen kommer fra leverandør A og er defekt, er 1,2%.
b)
$P(D)=P(D|A)\cdot P(A) + P(D|B)\cdot P(B) \\= 0,03\cdot 0,40 + 0,02 \cdot 0,60 = 0,012 + 0,012 = 0,024$
$P(A | D) = \frac{P(A) \cdot P(D|A)}{P(D)} = \frac{0,40 \cdot 0,03}{0,024} = \frac{0,012}{0,024} = 0,5 = 50\%$
Sannsynligheten for at en lader som er defekt, kommer fra leverandør A, er 50%.
Oppgave 6
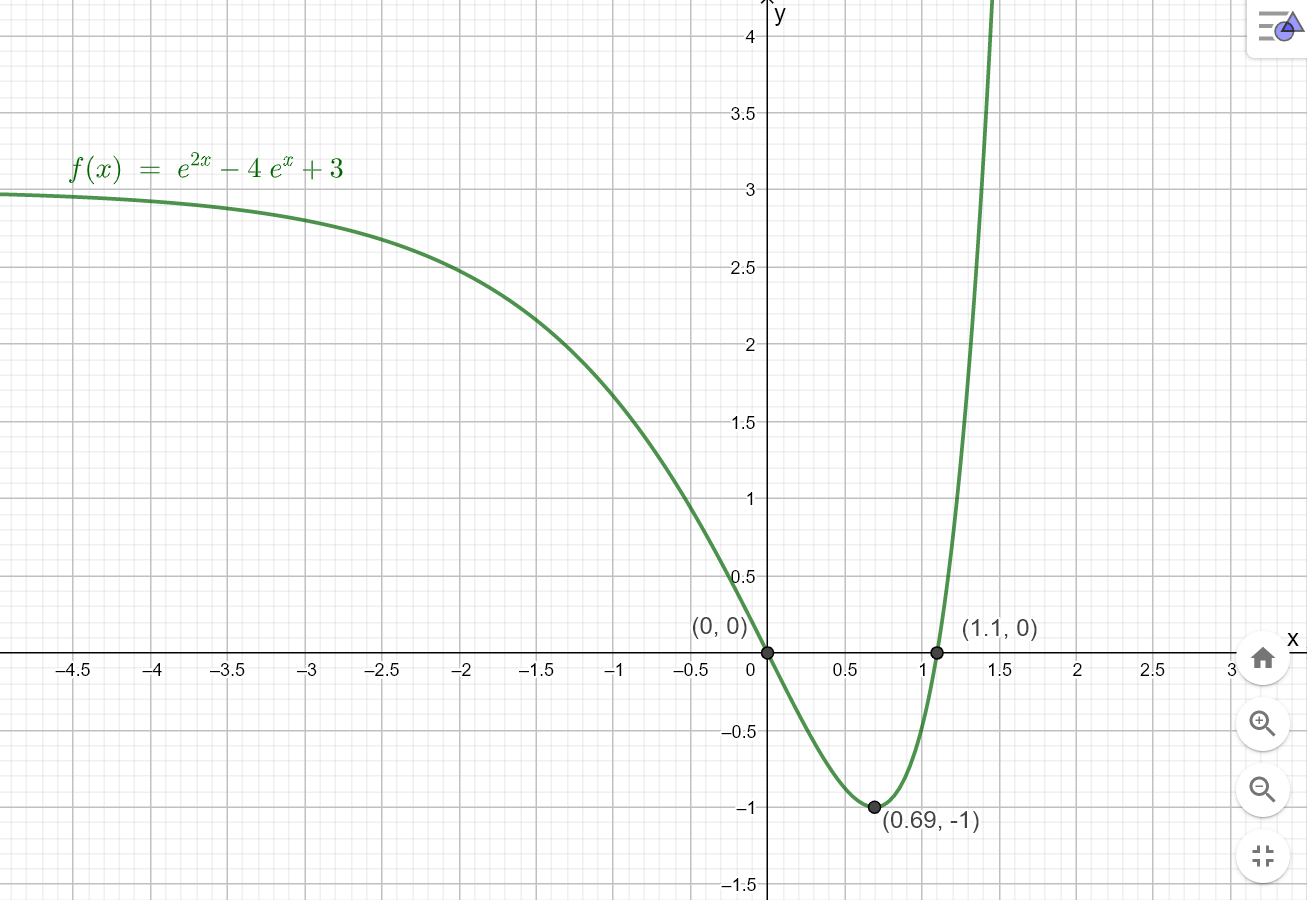
Vi har $f(x)=e^{2x}-4e^x+3$
a)
$f(x)=0 \\ e^{2x}-4e^x+3 = 0 \\ \text{Setter} \,u = e^x \\ u^2 - 4u + 3 = 0 \\ (u-1)(u-3)=0 \\ u= 1 \vee u = 3 \\ e^x = 1 \vee e^x = 3 \\ x = ln 1 \vee x = ln 3 \\ x = 0 \vee x \approx 1,10 $
Nullpunktene til f er (0,0) og (1.10, 0).
b)
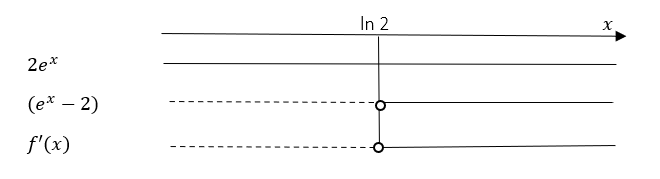
$f'(x)= 2e^{2x}-4e^x$
$f'(x)=0 \\ 2e^{2x}-4e^x = 0 \\ 2e^x(e^x-2)\\ 2e^x = 0 \vee e^x = 2 \\ \xcancel{x = ln 0} \vee x = ln 2 \\ x = ln 2 \approx 0,69$
Forkaster $x = ln 0$ da $ln 0 $ ikke er definert.
Finner funksjonsverdien i x = ln 2.
$f(ln 2) = e^{2(ln2)}-4e^{ln2} + 3 = e^{ln2^2}-4\cdot 2 + 3 = 4-8+3 = -1$
Grafen til f har et bunnpunkt i (0.69, -1).
c)
$f' '(x)=4e^{2x}-4e^x = 4e^x(e^x-1)$
$f' '(x)=0 \\ 4e^x(e^x-1) = 0 \\ 4e^x = 0 \vee e^x = 1 \\ \xcancel{x = ln0} \vee x=ln1 \\ x=0$
Finner funksjonsverdien i x = 0.
$f(0)=e^{2\cdot 0}-4e^0+3 = 1-4+3 = 0$
Grafen til f har et vendepunkt i (0,0).
d)
Du må tegne for hånd. Bruk nullpunktene og bunnpunktet fra de forrige oppgavene. Du regne noen omtrentlige funksjonsverdier for å få hjelp til å vite hvordan grafen går. I tillegg har vi at:
$\lim\limits_{x \to - \infty} f(x) = 3$
$\lim\limits_{x \to \infty} f(x) = \infty$
Oppgave 7
a)
For alle par av trekanter, har trekantene parvis like store vinkler, og forholdet mellom alle samsvarende sider er det samme. Alle trekantene er derfor formlike.
b)
Vi tar utgangspunkt i trekant ABD. Vinkelsummen i en trekant er 180 grader, altså er $\angle DAB + \angle BDA + \angle ABD = 180^{\circ}$.
Vi har $\angle DAB = \angle ADE$ fordi disse er samsvarende vinkler. Av samme grunn er $\angle ABD = \angle CDB$.
Det vil si at $\angle ADE + \angle BDA + \angle CDB = 180^{\circ}$, og punkt E, D og C ligger derfor på en rett linje.