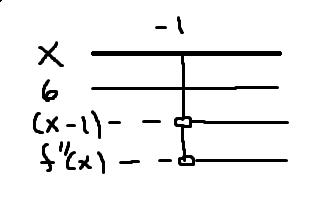Forskjell mellom versjoner av «S2 2015 høst LØSNING»
| Linje 1: | Linje 1: | ||
[http://matematikk.net/matteprat/viewtopic.php?f=13&t=41306 Diskusjon av denne oppgaven på matteprat] | [http://matematikk.net/matteprat/viewtopic.php?f=13&t=41306 Diskusjon av denne oppgaven på matteprat] | ||
| − | [http://matematikk.net/ | + | [http://matematikk.net/res/eksamen/S2/S2_H15_losn_tommyO.pdf Løsningsforslag laget av Tommy O.] |
| + | |||
==DEL 1== | ==DEL 1== | ||
Revisjonen fra 28. mai 2017 kl. 20:31
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av Tommy O.
DEL 1
Oppgave 1
a)
$f(x)=x^3+2x \\ f'(x)=3x^2+2$
b)
$g(x)=3e^{2x-1} \\ g'(x)=3e^{2x-1} \cdot (2x-1)'=6e^{2x-1}$
c)
$h(x)=x^2 \cdot e^x \\ h'(x)=2xe^x+x^2e^x=xe^x(2+x)$
Oppgave 2
a)
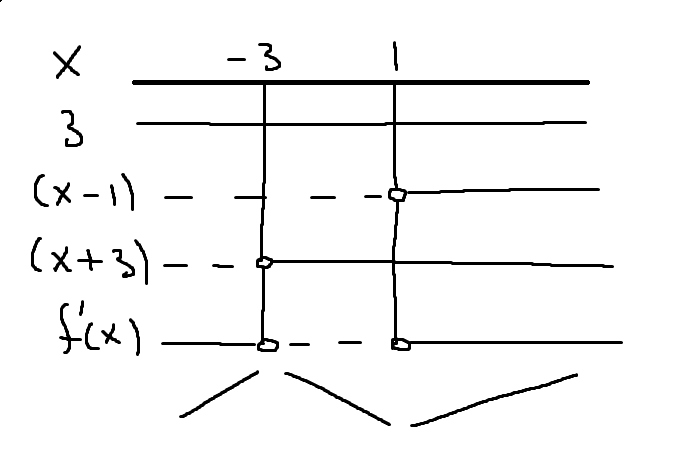
$f(x)=x^3+3x^2-9x \\ f'(x)=3x^2+6x-9=3(x^2+2x-3)=3(x-1)(x+3)$
Alternativt kan $f'(x)$ faktoriseres med ABC-formelen
Toppunkt: $T=(-3,f(-3))=(-3,-27+27+27)=(-3,27)$
Bunnpunkt: $B=(1,f(1))=(1,1+3-9)=(1,-5)$
b)
$ f ' ' (x)=6x+6=6(x+1) $
$6(x+1)=0$
$x=-1$
Vendepunkt: $V=(-1,f(-1))=(-1,-1+3+9)=(-1,11)$
c)
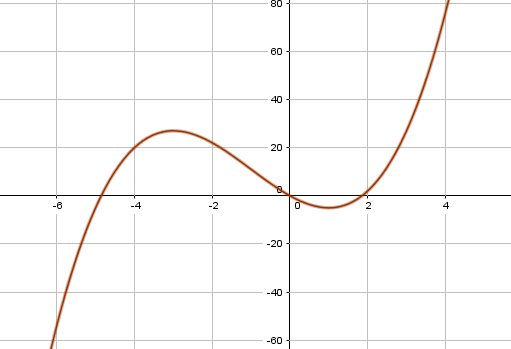
Utifra nullpunkter, ekstremalpunkter, vendepunkt og fortegnslinja til $f'(x)$ skal man kunne klare å lage en god skisse.
Oppgave 3
a)
$x^3-ax^2+2ax-8$ er alltid delelig med $(x-2)$ siden $2^3-2^2a+4a-8=0$
b)
Forkorter med polynomdivisjon.
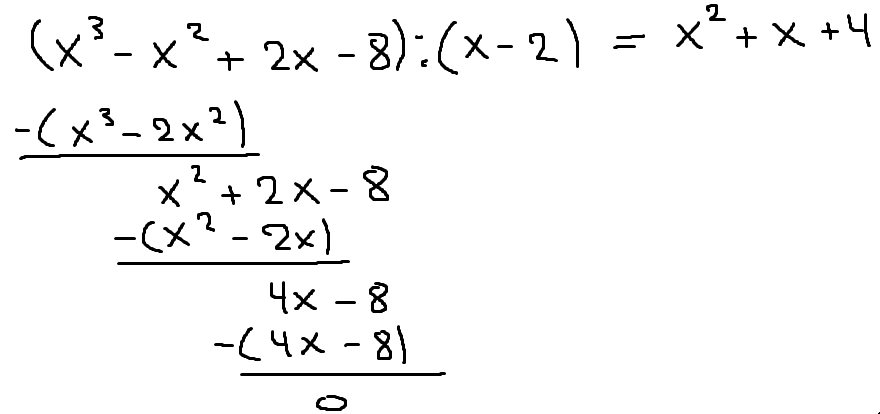
Oppgave 4
$ (1); \ x+2y-z=2 \\ (2); \ 2x-y+z=3 \\ (3); \ 3x-2y+2z=2 $
Her kan man bruke innsetingsmetoden eller adderingsmetoden. Jeg bruker adderingsmetoden. Fra $(1)$ og $(2)$.
$(4); \ (x+2y-z)+(2x-y+z)=3x+y=5$
Fra $(2)$ og $(3)$.
$-2(2x-y+z)+(3x-2y+2z)=-x=-2\cdot3+2=-4$
$x=4$
Fra (4). $y=5-3 \cdot 4=-7$
Fra (1). $z=x+2y-2=4+2\cdot-7-2=-12 $
$x=4 \ , \ y=-7 \ \ , \ z=-12 $
Oppgave 5
a)
$1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2^{n-1}}$
Dette er en geometrisk rekke siden den følger mønsteret $a_n=(\frac{1}{2})^{n-1}$
b)
$S_n=1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2^{n-1}}$
$S_n=\frac{a_1}{1-k}=\frac{1}{1-\frac{1}{2}}=2$
Oppgave 6
a)
$a_n=n^3+1 \\ a_1=2 \\ a_2=9 \\ a_3=28 \\ a_4=65$
b)
$\frac{a_1}{2}=1 \\ \frac{a_2}{3}=3 \\ \frac{a_3}{4}=7 \\ \frac{a_4}{5}=13$
c)
$\frac{a_n}{n+1}=\frac{n^3+1}{n+1}=\frac{(n+1)(n^2-n+1)}{n+1}=n^2-n+1$
Alternativt er det nok å si at $(n+1)$ er en av faktorene til $n^3+1$ siden $(-1)^3+1=0$
Oppgave 7
a)
Når de selger x enheter vil inntekten være $I(x)=x \cdot p(x)=480x-0.1x^2$
b)
$O(x)=I(x)-K(x)=(480x-0.1x^2)-(20000+120x+0.05x^2) \\ O(x)=360x-0.15x^2-20000$
$O'(x)=360-0.3x$
$360-\frac{3}{10}x=0 \Rightarrow x=\frac{360\cdot10}{3}=\frac{360}{3}\cdot10=1200$
(Viktig å tegne fortegnslinje for å vise at 1200 enheter gir et toppunkt og ikke et bunnpunkt.)
Oppgave 8
a)
( $P(X=a)$ er sannsynligheten for at spilleren ikke får gevinst. $X=a-200$ betyr at spilleren vinner 200 kr etter å ha betalt $a$ kr til kasinoet. )
En kan oppnå sum 10 på 3 forskjellige måter. (4,6 , 5,5 , 6,4)
$p(X=a-200)=\frac{3}{6^2}=\frac{3}{3\cdot12}=\frac{1}{12}$
En kan oppnå sum 7 på 6 forskjellige måter. (1,6 , 2,5 , 3,4 , 4,3 , 5,2 , 6,1)
$P(X=a-50)=\frac{6}{6^2}=\frac{1}{6}$
b)
I det lange løp vil spilleren tape $\frac{27}{36}$ av gangene, vinne 200 kr $\frac{1}{12}$ av gangene og vinne 50 kr $\frac{1}{6}$ av gangene.
$\frac{27}{36}a+\frac{1}{12}(a-200)+\frac{1}{6}(a-50)=5$
$a-\frac{200}{12}-\frac{50}{6}=5$
$a=5+\frac{200}{12}+\frac{50}{6}=5+\frac{150}{6}=5+25=30$
Da bør kasinoet sette prisen til 30 kr pr. spill.