Trigonometriske identiteter
Spisse vinkler
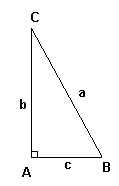
De trigonometriske funksjonene er sinus, cosinus, tangens. Vanligvis forkortes disse sin, cos, tan. For spisse vinkler defineres de trigonometriske funksjonene som forholdet mellom sidene i en rettvinklet trekant. Vi har:
DEFINISJONER
• <math>sin B = \frac ba </math>
• <math>cos B = \frac ca </math>
• <math>tan B = \frac bc = \frac{sin B}{ cos B}</math>
Enhetssirkelen - sin - cos - tan
De trigonometriske funksjonene begrenser seg ikke til spisse vinkler.
- Vi tegner en sirkel med radius 1.
- Positive vinkler kan tenkes framkommet ved en dreining mot klokken og negative vinkler fremkommer ved dreining med klokken.
- Dette kalles orienterte vinkler.
- I enhetssirkelen ser vi på orienterte vinkler med absolutte vinkelmål (radianer).
- Dersom en vinkel har høyre vinkelbein sammenfallende med positiv del av x aksen og toppunkt i origo sies vinkelen å være i grunnstilling.
Enhetsirkelen legges med sentrum i origo i et ortonormert koordinatsystem, slik at et av vinkelbeina er sammenfallende med den positive x aksen. Det andre vinkelbeinet skjærer sirkelen i punktet (x,y). De trigonometriske funksjonene defineres som følger:
$sin (a) = y \quad \quad cos (a) = x \quad \quad tan (a) = \frac yx $
Sin og cos har begge perioden $2\pi$. Tan har perioden $\pi$.
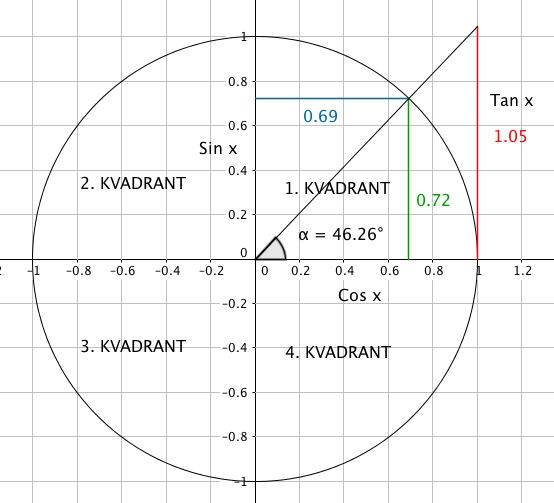
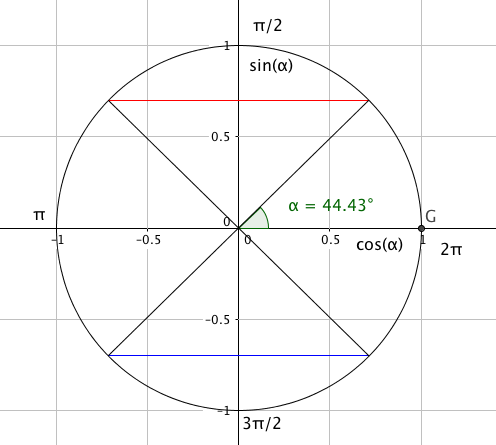
Enhetssirkelen og dens fire kvadranter:
Sinusverdien leses på y aksen (blå) og cosinus på x - aksen grønn.
En geometrosk tolkning av tangens ser du i den røde søylen. Dersom vinkelen ligger i 1. eller 4. kvadrant er lengden av linjestykket fra (1,0) langs linjen normalt på x -aksen, til skjæring med det andre vinkelbeinet. Tillsvarende i ( -1,0) for vinkler i 2. og 3. kvadrant.
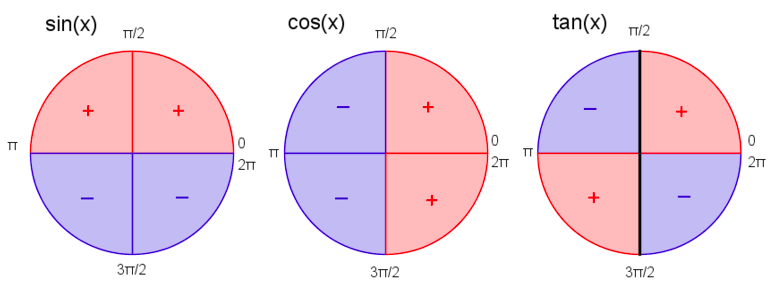
Figuren over viser fortegn på sin (x), cos( x) og tan (x) i de fire kvadrantene.
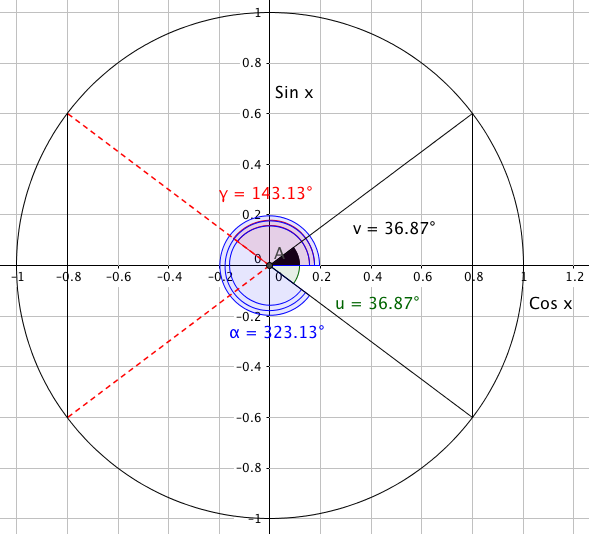
Fra enhetssirkelen ser man blant annet følgende om egenskapene til cosinus:
$v= -u \\ cos (v)= cos(-v) \\ cos (v) = cos (2 \pi - v) \\ cos v = - cos ( \pi - v)$
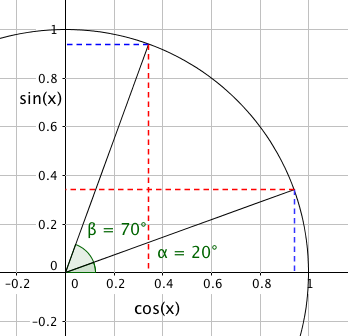
$cos (\alpha) = sin(\frac{\pi}{2}- \alpha) \\ sin (\alpha) = cos(\frac{\pi}{2} - \alpha)$
Fra enhetssirkelen ser man blant annet følgende om egenskapene til sinus:
$sin( \alpha) = - sin( - \alpha) \\ sin (\alpha) = sin (\pi- \alpha) \\ sin(\alpha) = sin(\alpha +2 \pi) \\ sin( \pi + \alpha)= sin (2\pi -\alpha)$
Identiteter
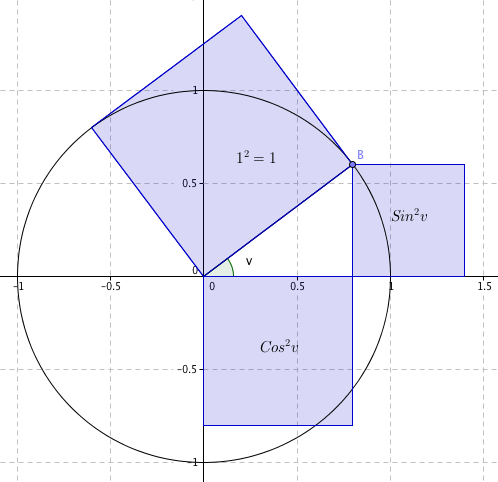
$sin^2v + cos^2v = 1\quad \quad \color{red}{(1)}$
Sum og differanser av vinkler
$cos(u-v) = cos(u)\cdot cos(v)+sin(u) \cdot sin(v) \quad \quad \color{red}{(2)} \quad \quad cos(u + v) = cos(u)\cdot cos(v)-sin(u)\cdot sin(v) \quad \quad \color{red}{(3)}\\ sin(u - v) = sin(u)\cdot cos(v)-cos(u)\cdot sin(v) \quad \quad \color{red}{(4)}\quad \quad sin(u + v) = sin(u)\cdot cos(v)+cos(u)\cdot sin(v)\quad \quad \color{red}{(5)}$
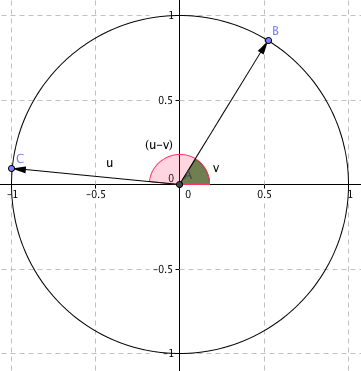
BEVIS (2):
Vinkelen (u-v) er vinkelen mellom vektorene $\vec{OB}$ og $\vec{OC}$ Begge disse har lengde en.
$\vec{OB}= [\cos v, \sin v] \\ \vec{OC} = [\cos u, \sin u]$
Skalarprodukt:
$ [\cos u, \sin u] \cdot [\cos v, \sin v] = 1 \cdot 1 \cdot \cos(u-v) \\ \cos(u-v) = \cos u \cos v + \sin u \sin v \quad \quad \color{red}{(2)}$
BEVIS (3):
$\cos(-v)= \cos v \\ \sin(-v) = - \sin v $
$\cos(u-v) = \\ \cos(u-(-v)) = \cos u \cos (-v) + \sin u \sin (-v) \\ \cos( u+v) = \cos u \cos v - \sin u \sin v \quad \quad \color{red}{(3)} $
BEVIS (5):
$ sin v = cos (90 - v) \\ sin (u + v) = cos (90 - (u+v)) \\ sin (u+v) = cos ((90-u)-v) \\ sin (u+v) = cos (90+u) cosv + sin(90-u)sinv \\ sin (u+v) = \sin u \cos v + \cos u \sin v \quad \quad \color{red}{(5)}$
BEVIS (4):
$ \sin (u+v)= \sin u \cos v + \cos u \sin v \\ \sin (u+(-v)) = \sin u \cos(-v) + \cos u \sin(-v) \\ \sin (u-v) = \sin u \cos v - \cos u \sin v \quad \quad \color{red}{(4)}$
Dobble vinkler
$sin(2u) = 2sin(u) \cdot cos(u) \quad \quad \color{red}{(6)} \\\ cos(2u) = cos^2u - sin ^2u \quad \quad \color{red}{(7)}$
<math>\cos(2u) = cos (u+u) \\ = \cos (u) \cos (u) - \sin (u) \sin (u)= \cos^2 (u) - \sin^2 (u) </math>
$cos(2u) = 2 cos^2 -1 (u)\quad \quad \color{red}{(8)}$
$ cos(2u) = 1 - 2 sin^2 (u)\quad \quad \color{red}{(9)}$
Dersom u + v = 180° har vi at Sin v = sin u og cos v = -cos u
Fra sum til produkt
$sin u + sin v= 2 sin ( \frac{u+v}{2}) cos ( \frac{u-v}{2})\quad \quad \color{red}{(10)}$
$sin u - sin v= 2 cos ( \frac{u+v}{2}) sin ( \frac{u-v}{2})\quad \quad \color{red}{(11)}$
$cos u + cos v= 2 cos ( \frac{u+v}{2}) cos ( \frac{u-v}{2})\quad \quad \color{red}{(12)}$
$cos u - cos v= - 2 sin ( \frac{u+v}{2}) sin ( \frac{u-v}{2})\quad \quad \color{red}{(13)}$
Fra produkt til sum
$sin u sinv = \frac 12[ cos (u-v) - cos (u+v)]\quad \quad \color{red}{(14)}$
$cos u cos v = \frac 12[ cos (u-v) + cos (u+v)]\quad \quad \color{red}{(15)}$
$sin u cos v = \frac 12[ sin (u+v) + sin (u-v)]\quad \quad \color{red}{(16)}$
$cos u sinv = \frac 12[ sin (u+v) - sin (u+v)]\quad \quad \color{red}{(17)}$
Flere funksjoner
De tre funksjonene som følger er ikke pensum i R2.
$ cot (a) = \frac xy \quad \quad sec (a) = \frac 1x \quad \quad cosec (a) = \frac 1y $
De tre neste er ikke pensum, men greie å kjenne til:
• <math>cot B = \frac cb = \frac{ cos B}{sin B} = \frac {1}{tan B}</math>
• <math>sec B = \frac ac = \frac{1}{cos B}</math>
• <math>cosec B = \frac ab = \frac{1}{sin B} </math>
$tan^2v + 1 = sec^2v\quad \quad\quad \quad \color{red}{(2)} \\ cot^2v+1 = csc^2v\quad \quad \color{red}{(3)}$
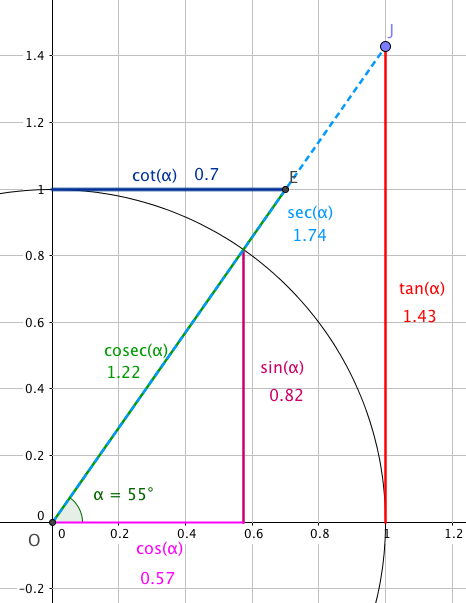
Geometrisk tolkning av de trigonometriske funksjonene. Figuren nedenfor viser de forskjellige trigonometriske funksjonene inntegnet i enhetssirkelen.
| Uttrykt ved | <math> \sin v\!</math> | <math> \cos v\!</math> | <math> \tan v!</math> | <math> \csc v\!</math> | <math> \sec v\!</math> | <math> \cot v\!</math> |
|---|---|---|---|---|---|---|
| <math> \sin v =\!</math> | <math> \sin v \! </math> | <math>\pm\sqrt{1 - \cos^2 v}\! </math> | <math>\pm\frac{\tan v}{\sqrt{1 + \tan^2 v}}\! </math> | <math> \frac{1}{\csc v}\! </math> | <math>\pm\frac{\sqrt{\sec^2 v - 1}}{\sec v}\! </math> | <math>\pm\frac{1}{\sqrt{1 + \cot^2 v}}\! </math> |
| <math> \cos v =\!</math> | <math>\pm\sqrt{1 - \sin^2 v}\! </math> | <math> \cos v\! </math> | <math>\pm\frac{1}{\sqrt{1 + \tan^2 v}}\! </math> | <math>\pm\frac{\sqrt{\csc^2 v - 1}}{\csc v}\! </math> | <math> \frac{1}{\sec v}\! </math> | <math>\pm\frac{\cot v}{\sqrt{1 + \cot^2 v}}\! </math> |
| <math> \tan v =\!</math> | <math>\pm\frac{\sin v}{\sqrt{1 - \sin^2 v}}\! </math> | <math>\pm\frac{\sqrt{1 - \cos^2 v}}{\cos v}\! </math> | <math> \tan v\! </math> | <math>\pm\frac{1}{\sqrt{\csc^2 v - 1}}\! </math> | <math>\pm\sqrt{\sec^2 v - 1}\! </math> | <math> \frac{1}{\cot v}\! </math> |
| <math> \csc v =\!</math> | <math> \frac{1}{\sin v}\! </math> | <math>\pm\frac{1}{\sqrt{1 - \cos^2 v}}\! </math> | <math>\pm\frac{\sqrt{1 + \tan^2 v}}{\tan v}\! </math> | <math> \csc v\! </math> | <math>\pm\frac{\sec v}{\sqrt{\sec^2 v - 1}}\! </math> | <math>\pm\sqrt{1 + \cot^2 v}\! </math> |
| <math> \sec v =\!</math> | <math>\pm\frac{1}{\sqrt{1 - \sin^2 v}}\! </math> |
<math> \frac{1}{\cos v}\! </math> | <math>\pm\sqrt{1 + \tan^2 v}\! </math> | <math>\pm\frac{\csc v}{\sqrt{\csc^2 v - 1}}\! </math> | <math> \sec v\! </math> | <math>\pm\frac{\sqrt{1 + \cot^2 v}}{\cot v}\! </math> |
| <math> \cot v =\!</math> | <math>\pm\frac{\sqrt{1 - \sin^2 v}}{\sin v}\! </math> | <math>\pm\frac{\cos v}{\sqrt{1 - \cos^2 v}}\! </math> | <math> \frac{1}{\tan v}\! </math> | <math>\pm\sqrt{\csc^2 v - 1}\! </math> | <math>\pm\frac{1}{\sqrt{\sec^2 v - 1}}\! </math> | <math> \cot v\! </math> |
Ved observasjon ser vi at fortegnet til en trigonometrisk funksjon varierer avhengig av hvilken kvadrant man befinner seg i. Nedenfor følger en oversikt.
| Kvadrant | I | II | III | IV |
| cos | pos | neg | neg | pos |
| sin | pos | pos | neg | neg |
| tan | pos | neg | pos | neg |
| cot | pos | neg | pos | neg |
| sec | pos | neg | neg | pos |
| cosec | pos | pos | neg | neg |