1P 2013 høst LØSNING
Del 1
Oppgave 1
Bruker "veien om 10%".
Vet at $30 \%$ er $150$ sider. Da er 10% $\frac{150 \text{ sider}}{3} = 50$ sider.
Hele boka er $100\% = 10 \cdot 10\%$. Dermed kan vi si at det er $10 \cdot 50 \text{ sider} = 500$ sider i boka til Per.
Oppgave 2
Målestokk: $\frac{2,0cm}{10km} = \frac{2cm}{10.000m} = \frac{2cm}{ 1.000.000cm} = \frac {1}{500.000} = 1: 500.000$
Oppgave 3
Areal av trapes: $A = \frac{10,0 m + 6,0 m}{2} \cdot 4,0 m = 8,0 m \cdot 4,0 m = 32,0 m^2 $
Oppgave 4
$\frac{\text{Reallønn}}{100} = \frac{\text{Nominell lønn}}{130} \\ 130 \cdot 500.00kr = NomLønn \cdot 100 \\ NomLønn = 1,3 \cdot 500.000 kr = 650.000 kr.$
Oppgave 5
Dette er en rettvinklet trekant.
Vi observerer at summen av arealene til kvadratene utspent av katetene er $25m^2 + 25m^2 = 50m^2$
I følge Pytagoras skal det være lik kvadratet utspent av hypotenusen. Dersom arealet hadde vært 49 kvadratmeter ville lengden av AB vært 7 meter. siden arealet er litt mer enn 49 kvadratmeter er AB lenger enn 7 meter.
Oppgave 6
$15m^3 = 15 000 dm^3 =15 000 liter \\ 4,2 timer = 4 timer + 0,2 \cdot 60 minutter = 4 timer + 12 minutter = 4 timer 12 minutter $
Oppgave 7
M = makspuls , A = alder. Vi har følgende modell:
$M = 211 - 0,64 \cdot A$
a)
Makspuls på en 20 åring:
$M = 211 - 0,64 \cdot 20 = 198,2$
En tyveåring har en makspuls på ca 198 slag per minutt.
b)
Alder når makspuls er 179 slag/minutt:
$M = 211- 0,64A \\ M - 211 = -0,64A \\ 0,64A = 211-M \\ A = \frac{211 - M}{0,64} \\ A = \frac{211 - 179}{0,64} = 50$
Svein er 50 år gammel.
Oppgave 8
a)
| Blå bukser | Svarte bukser | Total | |
|---|---|---|---|
| Bukser som passer | $3$ | $3 $ | $6$ |
| Bukser som ikke passer | $1$ | $3$ | $4$ |
| Total | $4$ | $6$ | $10$ |
b)
P (buksa passer) =$\frac {6}{10}$ = 60%
Det er 60% sjanse for at buksa passer.
c)
P ( blå bukse, gitt at den passer) = $\frac 36 = \frac 12 = $ 50%
Det er 50% sjanse for at buksa er blå, når vi vet at hun har trukket en bukse som passer.
Oppgave 9
a)
Grafen skjærer y aksen i 150kr. Da har vi null sjokolade, det betyr at en tom skål koster 150 kroner.
Når man leser av en graf må man være nøyaktig. Dersom man ser på 20 hektogram, ser man at grafen krysser 300 kroner akkurat. Det betyr at 20 hg koster 150kr. ( vi må jo trekke fra prisen på tom skål). 150kr : 20 hg = 7,50 kr/hg.
Altså koster sjokoladen 7,50 kr per hektogram.
b)
y = 7,5x + 150
Oppgave 10
Ja.
$ \frac{24 kr.}{0,4 kg.} = \frac{30 kr.}{0,5 kg.} = \frac{36 kr}{0,6 kg.} = 60 kr/kg$
Oppgave 11
Det betyr at ballens omkrets er ca. 200cm. Vi har at $O = \pi \cdot d$. Gjør et overslag og setter pi lik 3 og får at diameteren er $200 cm :3 \approx 65 cm$
Del 2
Oppgave 1
a)
$\frac{131,4}{123,1} = 1,067$ dvs. økningen er på 6,7%
b)
$\frac{8000}{128,8} = \frac{x}{131,4} \\ 8000 \cdot 131,4 = 128,8x \\ x= 8161,50$
Matvarene har økt i pris, til 8161,50 kr i 2012.
c)
Man sammenligner reallønna de to årene.
2008: $RL = \frac{45000kr}{123,1} \cdot 100 = 36555,65kr$
2012: $RL = \frac{49000kr}{131,4} \cdot 100 = 37290,70kr$
De hadde størst kjøpekraft i 2012.
Oppgave 2
a)
Begge sykler uten lys:
P ( begge uten lys) $= \frac{2}{10} \cdot \frac{2}{10} = \frac {4}{100} = 4$%
b)
Nøyaktig en uten lys. Det kan være den første vi velger, eller det kan være den andre vi velger:
P ( en uten lys)=$ \frac{2}{10} \cdot \frac{8}{10} + \frac{8}{10} \cdot \frac{2}{10} = \frac{32}{100} = 32$%
Oppgave 3
a)
$f(x)= 250000 \cdot 0,85^x \\ f(5)= 250000 \cdot 0,85^5 = 110926$
Bilen vil være verdt ca 111.000 kr. om fem år.
b)
Bilens verdi for fem år siden:
$x \cdot 0,85^5 =250000 \\ x= \frac{250000}{0,85^5} \\ x= 563444$
For fem år siden var bilens verdi ca. 565000 kroner.
Oppgave 4
a)
I en likesidet trekant er alle vinklene $60^{\circ}$. Vi observerer at vinkel ABC er summen av to slike vinkler, altså $120^{\circ}$
b)
Finn h ved hjelp av Pytagoras:
$h^2 = 3,0^2- 1,5^2 \\ h^2 = 9,0 - 2,25 \\h^2 = 6,75 \\ h = \sqrt{6,75} \\h=2,6$
Høyden er 2,6 cm.
c)
Finner først arealet av en likesidet trekant, multipliserer så med seks, for å finne arealet av hele sekskanten.
$A = \frac{g \cdot h }{2} \cdot 6 \\ A =\frac{3 \cdot 2,598 }{2} \cdot 6 \\A = 3,9 \cdot 6 \\ A= 23,4 $
Arealet av trekanten er $23,4 cm^2$.
Oppgave 5
a)
b)
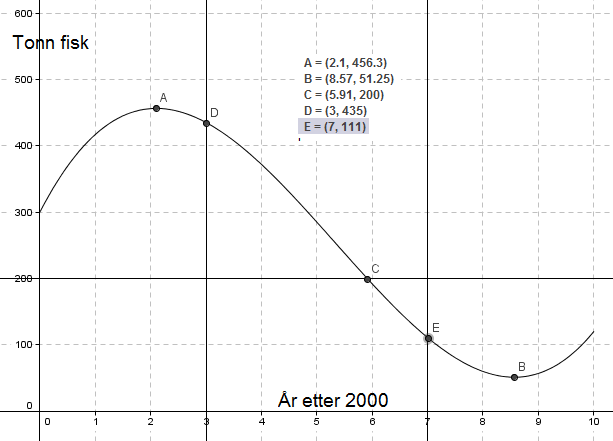
Fiskebestanden var minst sommeren 2008, da var den i overkant av 51 tonn.
c)
Koordinatene til skjæringspunktet er (5,91 , 200). Det betyr at bestanden var 200 tonn sent på høsten i 2005. Bestanden var på vei ned.
d)
Endring fra jan. 2003 til jan. 2007 var 111 tonn - 435 tonn = - 324 tonn. Perioden var fire år. Den gjennomsnittlige årlige endringen blir da: -324 tonn : 4år = - 81 tonn/år.
I denne perioden minket bestanden med 81 tonn i året, i gjennomsnitt.
Oppgave 6
a)
Månedslønn: $150timer \cdot 215kr/time = 32250kr$
Betaling til pensjonskassen er to prosent av dette: $32250 kr \cdot 0,02 = 643kr$
Han betaler kr. 645 til pensjonskassen denne måneden.
b)
Trekker fra fagforeningskontingent og innskudd til pensjonskassen og får skattbar inntekt: 32259 kr - 860 kr = 31390 kr
Runder ned til nærmeste hundre og får 31300 som ut fra tabellen gir et skattetrekk på kr. 9790,-
Oppgave 7
a)
Modellen består av en halvkule og en kjegle. Volum:
$V = \frac 23 \pi r^3 + \frac 13 \pi r^2h = \frac 23 \pi \cdot 0,60^3 + \frac 13 \pi \cdot 0,60^2\cdot(3,20-0,60) = 0,4524 + 0,9802 = 1,43$
Modellen har et volum på 1,43 kubikkmeter.
b)
Vi må altså finne modellens overflate, dvs. overflaten av halvkulen pluss overflaten av kjeglen, minus grunnflaten i kjeglen (den er under halvkulen).
$O_{modell} = \pi rs + 2 \pi r^2 = \pi \cdot 0,60 \cdot 2,67 + 2 \pi \cdot 0,60^2 = 5,03 + 2,26 7,29$
Modellens overflate er ca. 7,3 kvadratmeter. Dersom en boks maling dekker 2,2 kvadratmeter trenger man 7,3 : 2,2 = 3,3 bokser. I praksis 4 bokser maling.