2P eksempeloppgave 2015 vår LØSNING
- Løsningsforslag (pdf) fra joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
Har fått noen kommentarer til løsningsforslaget og har derfor rettet litt på det.
Del 1, oppgave 8b: Hadde klart å sette opp uttrykket med 12 år og ikke 20 år som oppgaven sa. Dette er rettet på.
Del 2, oppgave 2: Har lagt til en kort forklaring om bruk av Analyseknappen i Geogebra. Brukes denne kan oppgaven gjøre mye raskere.
Del 2, oppgave 3b: Hadde helt glemt ut å regne ferdig oppgaven. Slik det stod tidligere var det de som kjørte 10% saktere som var svaret og det er jo feil.
DELL EN
Oppgave 1
19 milliarder = $19 \cdot 10^9 = 1,9 \cdot 10^{10}$
$0,089 \cdot 10^{-6} = 8,9 \cdot 10^{-8}$
Oppgave 2
| Prosentvis endring | Vekstfaktor |
| + 8% | 1,08 |
| - 73% | 0,27 |
| - 83% | 0,17 |
| + 150% | 2,5 |
Oppgave 3
a)
$a^6 \cdot (a^4)^{-2} \cdot a^0 \\ = a^6 \cdot a^{-8} \cdot 1 \\ = a^{6-8} \\= a^{-2} \\ = \frac{1}{a^2}$
b)
$\frac{3^{-2} \cdot 9^3}{27^2} \\ = \frac{3^{-2} \cdot (3^2)^3}{(3^3)^2} \\ = \frac{3^{-2+6}}{3^6} \\ = 3^{-2+6-6} \\ = 3^{-2} \\ = \frac{1}{3^2} \\ = \frac 19$
Oppgave 4
a)
MEDIAN
Stigende rekkefølge:
0, 0, 2 ,2, 2, 3, 4, 5, 5, 5. Tallene som står i midten er 2 og 3 ( siden vi har 10 kamper, partall). Median blir da gjennomsnittet av 2 og 3 som er:
$\frac{2+3}{2} = 2,5$
GJENNOMSNITT
$Gj = \frac{0+ 0+ 2 +2+ 2+ 3+ 4+ 5+ 5+ 5}{10} = 2,8$
b)
Da legge vi sammen antall kamper med 0 mål, 1 mål og 2 mål. Det er ingen med 1 mål, så tilsammen blir det 2 + 3 = 5. Den kumulative frekvensen for 2 mål er 5. Det betyr at i 5 kamper ble det scoret 2 eller færre (mindre) mål.
Oppgave 5
Prisen er x i begge butikker. Bruker vekstfaktor:
Butikk A: $x \cdot 1,2= 1,2x$
Butikk B: $(x \cdot 1,1) \cdot 1,1 = 1,21x$
Varen er dyrest i butikk B fordi grunnlaget for den siste 10% økningen ikke er x, men 1,1x.
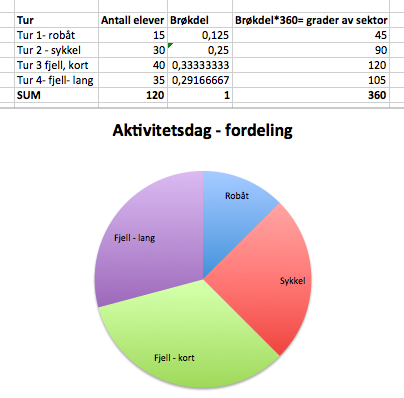
Oppgave 6
Oppgave 7
| Antall minutter | Antall elever - f | Klassemidtpunkt m | $f \cdot m$ |
| [0, 30> | 10 | 15 | 150 |
| [30, 60> | 30 | 45 | 1350 |
| [60,120> | 50 | 90 | 4500 |
| [120, 240> | 10 | 180 | 1800 |
| Sum | 100 | 7800 |
Man forutsetter at elevene fordeler seg jevnt utover i de respektive intervaller. Gjennomsnittet blir da 7800 / 100. En elev bruker i gjennomsnitt 1 time og 18 minutter på matematikkleksen, per uke.
Oppgave 8
a)
Av 500 liter forsvinner 2% hvert år i 12 år:
$f(12)=500 \cdot 0,98^{12}$
b)
Det som har fordampet = 500 - det som er igjen.
$g(20) = 500 - 500 \cdot 0,98^{20}$
Oppgave 9
De svømmer I et 25 meters basseng. Kine er presis i starten og vender først, etter ca 18 sekunder. Mina vender etter ca 25 sekunder og har de siste 10 meterne tapt mye i forhold til Kine. Kine svømmer bra til det er ca 17 meter igjen, da sprekker hun og blir forbisvømt av Mina etter 30 sekunder, 15 meter før mål. Mina kommer i mål etter ca. 46 sekunder og Kine etter ca. 56.
Oppgave 10
a)
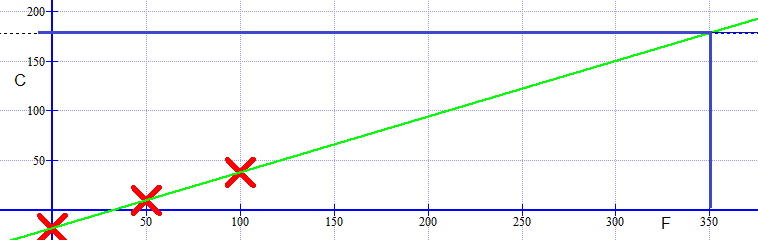
| $^\circ$F | 0 | 50 | 100 |
| $^\circ$C | -18 | 10 | 38 |
b og c)
Kaka skal stekes på $178^\circ C$
DEL TO
Oppgave 1
a)
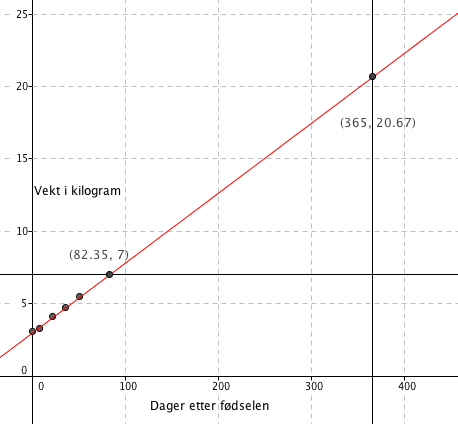
b)
Fra figuren i aser man at det tar ca 83 dager før han veier 7 kilogram.
c)
Modellen overestimerer vekten med i størrelsesorden 100% etter ett år, siden blir det verre. Den er nok bare relativt god for de første 3-4 måneder.
Oppgave 2
a)
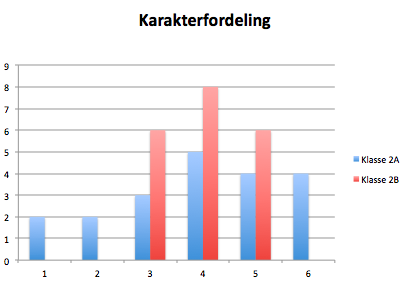
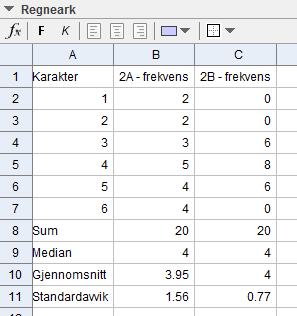
b)
Begge klassene har samme median og nesten samme gjennomsnitt, men A klassen har mye større spredning, med karakterer over hele skalaen, derfor det store standardavviket.
Oppgave 3
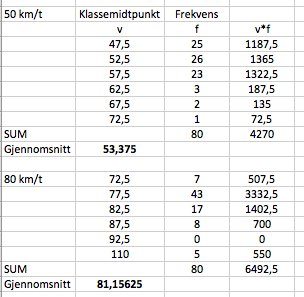
a)
Gjennomsnittsfarten er henholdsvis 53,4 km/t og 81,2 km/t.
b)
50 km/: 10% av 50 er 5. Vi er ute etter de bilene som kjører 55 km/t, eller fortere. Ved opptelling ser man at det er 23 + 3+ 2 + 1 = 29, av totalt 80 biler.
Det er ca. $\frac{29}{80} \cdot 100$% = 36,3% som kjører 10% eller mere, over fartsgrensen i 50 sonen.
80 km/t: 10% av 80 er 8. Vi er nok en gang ute etter de bilene som kjører 88 km/t, eller fortere. Man observerer at 88 ligger i intervallet [85,90>. Vi forutsetter at bilene i dette intervallet fordeler seg jevnt utover. Vi er da interessert i bilene i de to øverste delene, av fem, i intervallet, og får:
$\frac{2}{5}\cdot 8 \approx 3$ . Det er ca 3 biler i dette intervallet som ligger over 88 km/t. I tillegg har vi 5 som kjører veldig fort, så totalt er det 8 biler av 80 som ligger 10% eller mere over fartsgrensen. Det tilsvarer ca 10% av bilene.
Oppgave 4
a)
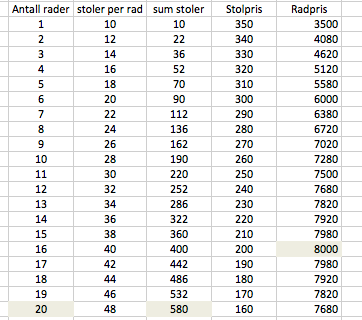
Løses lettest i regneark:
Det er 20 stolrader i salen.
Alternativ dersom du liker å tenke bedre enn å taste i et regneark:
I denne type oppgaver må vi se etter mønster og systemer. Det er om å gjøre å knytter radnummer opp mot antall seter. Vi har:
10, 12, 14, 16, 18, .... Som kan skrives
10, 10 + 2, 10 + 4, 10 + 6, 10 + 8,....
Vi ser at det siste leddet kan skrives som 2n-2, er man på rad tre (n=3) er det 10 + 6 - 2 stoler. Det gir oss en sammenheng
Stoler = $10+2n-2 = 2n+8$ , da har vi et utrykk for antall stoler på rad nummer n.
Summen av stoler i salen blir antall stoler på første rad, pluss antall stoler på rad n (siste rad) delt på 2 (finner da gjennomsnittet). Dette multipliseres med antall rader n. Oversatt til matematikk ser det slik ut:
$\frac{10 + (2n+8)}{2} \cdot n = n^2+9n$
Vi vet at antallet stoler i salen er 580 og må da løse $n^2+9n - 580 =0 $ Bruk graftegner i Geogebra. En løsning vil være 20.
b)
Fra regnearket i a ser man at rad 16 er dyrest, 8000 kroner for hele raden.
Oppgave 5
a)
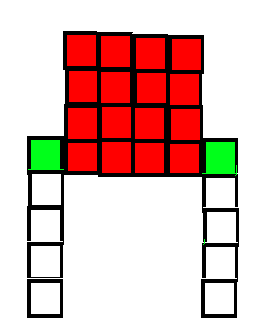
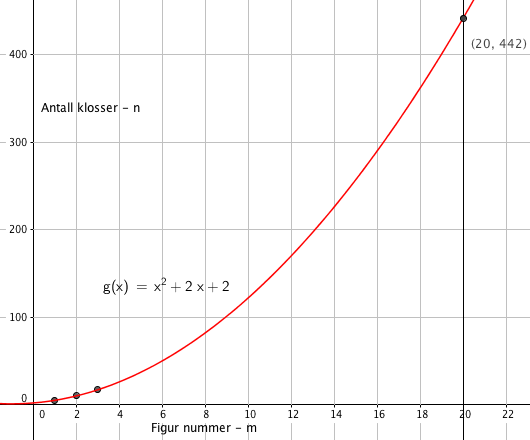
Dette er Figur nummer fire, da må man prøve å uttrykke antall klosser med noe med 4 i. Det røde kvadratet er $4^2= 16$. så er der to "ben", med 4 klosser i hver (markert hvitt), det blir $2 \cdot 4$. Så er det to grønne klosser til overs.
Antall klosser blir da:
$4^2+2 \cdot 4 +2 =26$
Eller en formel som gjelder generelt: $A(n)= n^2+2n+2 \\ A(5) = 25+10+2=37 \\ A(6) = 36+ 12 +2 = 50$
b)
Jeg kalte den A i stedet for m, men modellen er altså
$m_n=n^2+2n+2 \\ m_{20} = 400 + 40 +2 =442$
Oppgave 6
a)
Lengde av gjerde:
$4x+2y=500 \\ y= 250-2x$
Areal:
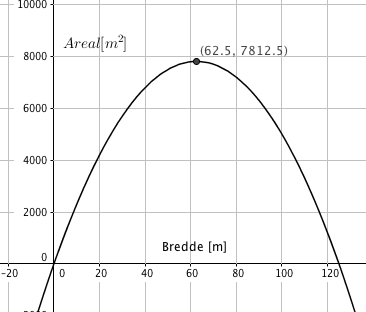
$A=xy \\ A(x)= x(250 - 2x) \\ A(x) = -2x^2+250x$
b)
Arealet blir størst når x = 62,5 meter. Da er arealet 7812,5 kvadratmeter.
Oppgave 7
a)
1) En reduksjon på 11% per time gir etter en time:
$220mg \cdot 0,89 = 196mg $
2) Etter åtte timer:
$220mg \cdot 0,89^8 = 87mg $
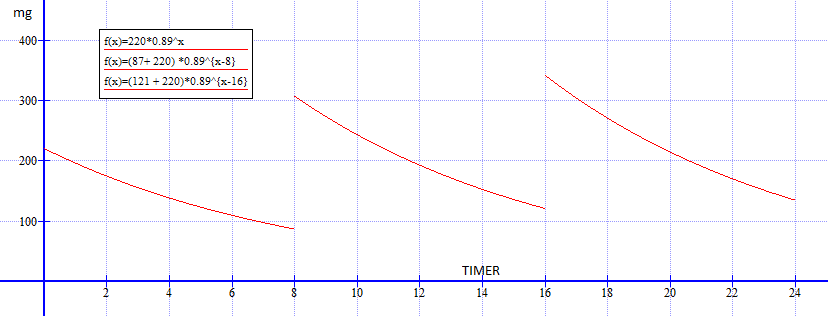
b)
1) Her går vi ut fra at antibiotikaen blir tatt opp i kroppen med en gang. I virkeligheten tar det lengre tid.
Hun har 87mg fra første tablett pluss 220mg fra den nye tabletten, dvs. ca 307 mg. antibiotika.
2)
Når hun tar den tredje tabletten har hun en liten rest fra den første tabletten i kroppen, en litt større rest fra den andre og 220mg fra den tredje:
$220 \cdot 0,89^{16} + 220 \cdot 0,89^8 + 220 = 220(0,89^{16} + 0,89^8 + 0,89^0) = 220 + 87 + 34 = 341$mg