Introduksjon til differensiallikninger
Innledning
En differensialligning vil typisk beskrive en forandring av en variabel i tid og/eller rom. Den skiller seg fra "vanlige" ligninger ved at løsningene er funksjoner, ikke bestemte verdier. Teorien for differensialligninger er fundamental for forståelsen av dynamikken i naturen og danner grunnlaget for blant annet klassisk mekanikk og kvantemekanikk. Vi deler diff.ligningene inn i partielle og ordinære ligninger, der matematikken i videregående skole kun fokuserer på ordinære ligninger, ofte kalt ODE (Ordinary Differential Equations). Dvs. at løsningsfunksjonen kun har én variabel, som oftest kalt $t$ (for tid) eller $x$ (for rom). Det er vilkårlig hvilken notasjon vi bruker så lenge vi er bevisst på hva som er den ukjente funksjonen og hva som er variabelen.
- På ungdomstrinnet og videregående grunnkurs arbeidet man med ligninger der den ukjente var et tall, ofte kalt $x$.
- I differensialligninger er den ukjente en funksjon $y(x)$. En differensialligning gir sammenhengen mellom en ukjent funksjon og noen av dens deriverte.
- I denne artikkelen skriver vi $y^\prime$ og $\frac{dy}{dx}$ om hverandre. Den siste skrivemåten kalles Leibniz' notasjon etter den tyske filosofen og matematikeren Gottfried Wilhelm Leibniz.
- Man bør være fortrolig med ligninger, funksjonslære, integrasjon og derivasjon før man gir seg i kast med differensialligninger.
- Ligningene er viktige i fysikk og andre fag, der de kan brukes til å modellere forskjellige situasjoner der størrelser forandrer seg over tid.
Ordenen til en diff.ligning
Formelt vil en ordinær diff.ligning være på formen <math>g(x,f,f^\prime ,f^{\prime \prime},\ldots , f^{(n)})=0</math> der <math>g</math> er en gitt funksjon. <math>n</math> kalles ligningens orden og <math>f^{(n)}</math> er den n-te deriverte. <math>f</math> er her den ukjente funksjonen som vi ønsker å finne, og <math>x</math> er variabelen som vi deriverer med hensyn på, dvs. <math>f^\prime \equiv \frac{df}{dx}</math>, <math>f^{\prime \prime} \equiv \frac{d^2f}{dx^2}</math>, etc.
Eksempel: Diff.ligning av første orden
En enkel ordinær differensialligning av første orden er <math>f^{\prime}(x)=0</math>. Løsningen finnes direkte ved integrasjon; vi får at <math>f(x)=c</math> for en konstant <math>c</math>.
Eksempel: Diff.ligning av 2.orden
En enkel andreordens ordinær differensialligning er <math>m\ddot{x}(t)=10</math>. Dette er Newtons andre lov med konstant kraft (10 N) der <math>x(t)</math> er posisionen ved tida <math>t</math>. De to prikkene over <math>x</math> betyr at vi dobbeltderiverer <math>x</math> med hensyn på tiden.
Førsteordens lineære ligninger
Lineære differensialligninger av første orden kan skrives på formen
\begin{equation} \label{linearEqFirstOrder} y' + ay = b \end{equation}
Her er $a$ og $b$ enten gitte konstanter, eller funksjoner av $x$. At en ligning er av første orden betyr at den inneholder den førstederiverte, $y'$, men ikke deriverte av høyere orden ($y^{\prime\prime}$, $y^{(3)}$ etc.). At en ligning er lineær betyr at $y$ og $y'$ inngår som lineære faktorer i leddene. Ligningen $y'+y^2=3$ vil f.eks. ikke være lineær siden vi har et ledd med $y^2$.
Homogene og inhomogene førsteordens diff.ligninger
Dersom $b\neq 0 $ i ligning kalles den inhomogen. Dersom $b = 0$ kalles diff.ligningen homogen. En homogen, lineær diff.ligning av første orden er altså på formen
\begin{equation} \label{linearHomEqFirstOrder} y' + ay = 0 \end{equation}
Slike ligninger kan løses på to måter:
- Multiplikasjon med integrerende faktor
- Som en separabel ligning
Integrerende faktor
Når vi bruker integrerende faktor tenker vi multiplikasjonsregelen for derivasjon, baklengs. Vi omformer da to ledd til et produkt. Den integrerende faktorene er $e^{ax}$ der a er a'en i $y' + ax = b$
Vi skal løse $y'+2y = 0$. Integrerende faktor er $e^{2x}$.
\begin{align*} y'+2y & = 0 \\ e^{2x}y'+2e^{2x}y & = 0 \quad \text{Multiplisert med integrerende faktor}\\ (e^{2x}y)' & = 0 \\ e^{2x}y & = C \\ y & = Ce^{-2x} \end{align*}
For å finne ut hva $C$ er trenger man i tillegg en initialbetingelse (startbetingelse) på løsningen. Det behandles i avsnittet om Initialverdiproblemer.
Vi skal løse $y'+4y = 6$. Integrerende faktor er $e^{4x}$.
\begin{align*} y'+4y & = 6 \\ e^{4x}y'+4e^{4x}y & = 6e^{4x} \quad \text{Multiplisert med integrerende faktor}\\ (e^{4x}y)' & = 6e^{4x} \\ e^{4x}y & = \int 6e^{4x}\,dx\\ e^{4x}y & = \frac{3}{2}e^{4x}+C\\ y & = \frac{3}{2}+Ce^{-4x} \end{align*}
For å finne ut hva $C$ er trenger man i tillegg en initialbetingelse (startbetingelse) på løsningen.
Separable differensiallikninger
Separable ligninger er på formen
\begin{equation} \label{separableDiffEq} \frac{dy}{dx} = g(x)\cdot h(y) \end{equation}
, der $g(x)$ og $h(y)$ er gitte funksjoner som vanligvis er relativt enkle å integrere. Merk at funksjonsargumentet til $h(y)$ er den funksjonen vi skal finne, men vi behandler likevel $y$ som en vanlig variabel. Ligningen løses ved å multiplisere med differensialet $dx$ på begge sider av likhetstegnet, dividere med $h(y)$, for så å integrere. Vi kan løse en generell separabel ligning formelt slik:
\begin{align*} \frac{dy}{h(y)} &= g(x)\,dx \\ \int \frac{dy}{h(y)} &= \int g(x)\,dx \\ F(y) &= G(x) + C \\ y(x) &= F^{-1}\left(G(x) + C\right) \end{align*}
, der $F(y)$ er integralet av $(h(y))^{-1}$ og $G(x)$ integralet av $g(x)$. $C$ er en integrasjonskonstant og $F^{-1}$ er inversfunksjonen til $F$.
Vi skal løse ligningen $y'+4xy=0$ som en separabel ligning. Da er det lurt å bruke Leibniz' notasjon. Vi omskriver til: \begin{align*} \frac{dy}{dx} &=-4xy \\ \frac{dy}{y} &=-4x\,dx \\ \int{\frac{dy}{y}} &=\int{-4x\,dx} \\ \ln|y| &= -2x^2 + C \\ y &= e^{-2x^2 + C} \\ y &= y_0 \cdot e^{-2x^2} \end{align*}
Her har vi omdøpt konstanten foran eksponentialfunksjonen, slik at $y_0=e^C$. Ved å sette løsningen inn i den opprinnelige diff.ligningen, ser vi at løsningen stemmer.
Homogene lineære andreordens diff.ligninger med konstante koeffisienter
En generell andreordens diff.ligning er på formen
\begin{equation} A(x)y^{\prime\prime} + B(x)y' + C(x)y = D(x) \end{equation}
- Ligningen er homogen dersom $D(x) = 0$. Det gir oss <math>A(x)y^{\prime\prime} + B(x)y' + C(x)y = 0</math>
- Konstante koeffisienter betyr at $A(x)$, $B(x)$ og $C(x)$ er konstanter uavhengig av $x$. Vi skriver ligningen på formen $y^{\prime\prime} + by' + cy = 0$
- Andreordens betyr at den dobbelderiverte opptrer i ligningen. I en tredjeordens ligning vil den tredjederiverte opptre.
- Lineær betyr at produkter eller potenser av $y$ og dens deriverte ikke forekommer i ligningen. $y^{\prime\prime} = yy'$ er således et eksempel på en ikkelineær ligning.
- Karakteristisk ligning til $y^{\prime\prime} + by' + cy = 0$ er $r^2+br + c = 0$
Den karakteristiske ligningen kan ha tre ulike typer løsninger:
- To ulike reelle røtter
- Én reell rot
- To komplekse røtter
<math>y(x) = C_1e^{r_1x} + C_2e^{r_2x}</math>
<math> y^{\prime\prime} + y' = 2y \\ y^{\prime\prime} + y' - 2y = 0 \\ r^2 + r - 2 = 0 \\ r = 1 \vee r = 2 \\ y(x) = C_1e^x + C_2e^{2x}</math>
$4y^{\prime \prime} + 8y' + 4y =0 \\r^2 + 2r + 1 = 0 \\r = -1\\y(x) = C_1e^{-x} + C_2xe^{-x}$
Dersom ligningen har to komplekse røtter, <math>r_1 = a + ib</math> og <math>r_2 = a - ib</math>, blir løsningen
<math>y(x) = e^{ax}\left (C_1 \cos(bx) + C_2 \sin (bx)\right )</math>
<math>y^{\prime\prime}-y' + y = 0 \\ r^2 - r + 1= 0 \\ r_1 = \frac12 + \frac32i, \quad r_2 = \frac12 - \frac32i \\ y(x) = e^{\frac12x}\left (C_1 \cos(\frac32x) + C_2 \sin (\frac32x)\right )</math>
Initialverdiproblemer
I eksemplene over (og senere) ser man at den generelle løsningen inneholder en eller to konstanter $C_1$ og $C_2$. Disse kan i utgangspunktet være et hvilket som helst reelt tall. For å finne den spesielle løsningen til en ligning trenger man en eller flere tileggsopplysninger.
Når en differensialligning er gitt med initialbetingelser kalles det for et initialverdiproblem.
Initialbetingelsen(e) kan være knyttet til situasjonen ved tiden $t = 0$, altså når en prosess starter, eller den kan gis i form av en funksjonsverdi for en annen argumentverdi.
<math>\frac{dy}{dx} = 3x + 2 \hspace{50 mm} y (1)= 3 \\ dy = (3x + 2)\,dx \\ y(x) = \int 3x + 2 \,dx \\ y(x) = \frac 32x^2 + 2x + C </math>
Dette er den generelle løsningen.For å finne den spesielle løsningen benytter vi opplysningen
$y(1) = 3$.<math>y(1) = \frac 32 \cdot 1^2 + 2 \cdot 1 + C = 3 \\ C = - \frac 12 </math>
Den spesielle løsningen blir:<math>y(x) = \frac 32 \cdot x^2 + 2 x - \frac 12 </math>
Retningsdiagram
Førsteorden ligninger kan skrives som $y'(x) = F(x,y)$ der $x$ er den variable og $y$ er den ukjente
funksjonen. Dette gir stigningstallet til tangen i punktet $(x,y)$. Dette gir et bilde av hvordan grafene til løsningsfunksjonene ser ut og kalles et retningsdiagram for differensialligningen.
På engelsk er betegnelsen "slope field".
Utfra retningsdiagrammet får vi også et bilde av hvordan ulike integralkurver ser ut.
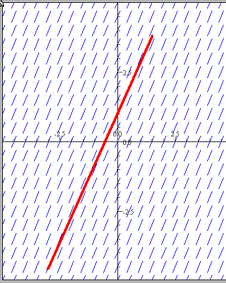
Eksempel: Retningsdiagram
Gitt er ligningen $y' = 2$
Vi observerer at stigningstallet til $y(x)$ er $2$ for alle $x$. Løsningen på ligningen er en eller
annen rett linje med stigningstall $2$. Et retningsdiagram illustrerer dette:Dersom man løser ligningen $y' = 2$
får man $y = 2x + C$, når man integrerer på begge sider.
Vi ser nå at retningsdiagrammet stemmer: $C$ skyver grafen opp eller ned i koordinatsystemet. Verken $x$ eller $y$ har noen betydning for grafens form. Diagrammet indikerer en løsning for $y = 2x + 1$
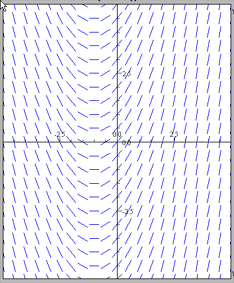
Eksempel: Retningsdiagram
Gitt er ligningen $y' = x + 1$
Man observerer at stigningstallet til $y(x)$ varierer med varierende $x$-verdi, og er $0$ for $x = -1$. Det gir følgende retningsdiagram: $\\$
$\\$
Dersom man løser ligningen $y' = x + 1$ får man <math> y = \frac 12x^2 + x + c </math> når man integrerer på begge sider.
Retningsdiagrammet indikerer at løsningen er en parabel med minimum i $x = -1$.