Ulikheter
Innledning
Ulikhetstegnene < og > brukes til å fortelle at en størrelse er mindre eller større enn en annen.
x > y leses ”x er større enn y”
x < y leses ” x er mindre enn y”
I tillegg har man tegnene <math>\geq</math> som leses "...større eller lik..... ", og <math>\leq</math> som leses "...mindre eller lik...".
Ulikheter løses som ligninger med et viktig unntak:
- Dersom man multipliserer eller dividerer hvert ledd i en ulikhet med samme negative tall, må ulikhetstegnet snus.
Eks 1:
4 > 2
Usagnet forteller oss at fire er større enn to, noe som er riktig ut fra vår forestiling om tallenes verdi. Dersom vi multipliserer utrykket med -1 får vi:
-4 < -2Vi har snudd ulikhetstegnet og observerer at utsagnet er riktig fordi -4 er mindre enn -2.
Enkle ulikheter
Ulikheter der deler av x (i første) inngår løses som en ligning. Alle ledd med x samles på venstre side og trekkes sammen, og alle tall samles på høyre side og trekkes sammen.
Eks 2:
4x -2 > 10 – 2x
4x +2x > 10 + 2
6x > 12
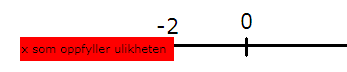
x > 2
I eksempel 2 har vi kun brukt de samme reglene som gjelder for behandling av ligninger.
Legg merke til at det er uendelig mange x verdier som passer i ulikhetene i eksempel 2 og 3.
Eks 3:
17x + 10 > 30 + 27x
17x - 27x > - 10 + 30
- 10x > 20
-x > 2x < -2
Eksempel 3 viser det grep som er spesielt for ulikheter; når man multipliserer eller dividerer med et negativt tall må man snu ulikhetstegnet.
En viktig konsekvens av dette er at man ikke uten videre kan multiplisere begge sider av ulikheten med x, fordi man ikke vet om man multipliserer med en positiv eller negativ størrelse.
Fortegnsskjema
Poenget med et fortegnsskjema er å klargjøre for hvilke x - verdier et utrykk er positivt og for hvilke verdier det er negativt. Dette gjør man ved å faktorisere uttrykket for så å tegne en fortegnslinje for den enkelte faktor.
Eks 4:
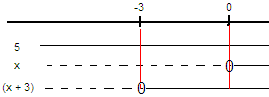
La oss se på utrykkene 5, x og (x + 3). Vi ønsker å tegne et fortegnsskjema for hvert av de tre uttrykkene.
Man markerer negative verdier med en stiplet linje og positive verdier med en heltrukket linje.
- 5 er et positivt tall og verdien er positiv uavhengig av eventuell x verdi.
- x er en variabel som skifter fortegn ved 0.
- Uttrykket x+3 er negativt fra minus uendelig til -3. I -3 er uttrykket null. For verdier større enn – 3 er uttrykket positivt.
Rasjonale funksjoner (brøkfunksjoner)
Eks:5
Ulikheten:
<math> \frac{x+2}{x-1}\leq 0 </math>
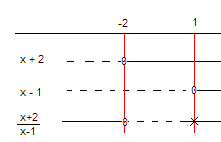
løses ved hjelp av at fortegnsskjema. Vi lager en fortegnslinje for hver faktor i brøken. I dette tilfellet er det en faktor i teller og en i nevner:
Fra skjemaet ser man at telleren skifter fortegn i x = – 2 og har verdien 0 i dette punkt.
Nevner er null i x = 1, der den skifter fortegn.
Det er viktig å merke seg at brøken ikke er definert for x=1 fordi verdien av nevneren er null.
Brøken er null når telleren er null, i -2.
Fra skjemaet leser vi at brøken er mindre eller lik null i <math> x \in [-2,1> </math>
Eks 6:
<math> \frac2x + 3 < \frac{3x}{x-1} \\ \frac{2+3x}{x} - \frac{3x}{x-1} < 0 \\\frac{2(x-1)+3x(x-1) - 3x\cdot x}{x(x-1)} < 0 \\ \frac{2x-2 -3x}{x(x-1)} < 0 \\ \frac{-x-2}{x(x-1)} < 0 </math>
Regler:
- Flytt og bytt slik at alle ledd står på venstre side og null på høyre side.
- Finn fellesnevner og trekk sammen til en brøk.
- Faktoriser teller og nevner.
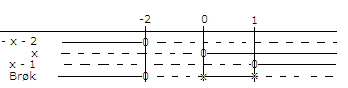
- Tegn fortegnslinjer for hver av faktorene
- Finn fortegnslinjen til brøken
HUSK: Når nevner er null er brøken IKKE definert. Når teller er null er brøken null.
Andregradsuttrykk
<math>ax^2 + bx +c > 0</math>
Ulikheten løses ved å faktorisere 2. gradsuttrykket og tegne fortegnsskjema for hver enkelt faktor.
Eks 7:
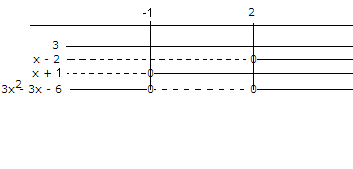
<math>3x^2< 3x + 6 \\ 3x^2 - 3x - 6 < 0 \\ 3(x-2)(x+1) <0</math>
Fra fortegnsskjemaet ser man at ulikheten er mindre enn null fra x større enn - 1 til x mindre enn 2. Eller:
<math>x \in <-1,2></math>
En ulikhet kan gjerne bestå av en brøk som inneholder et andregradsuttrykk. Man ordner ulikheten slik at man får et uttrykk med null på høyre side. Uttrykket på venstre side må faktoriseres:
Eks. 8:
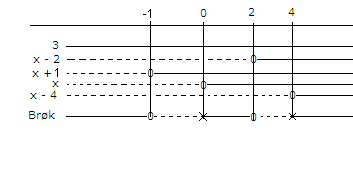
<math> \frac {3x^2 - 3x - 6}{x^2-4x}>0 \\ \frac {3x^2 - 3x - 6}{x^2-4x}>0 \\ \frac {3(x-2)(x+1)}{x(x-4)}>0 </math>
Man er ute etter de x - verdier som gjør at uttrykket er positivt. <math> x \in < \leftarrow , -1> \cup <0,2> \cup <4, \rightarrow> </math>