Forskjell mellom versjoner av «R1 2012 vår LØSNING»
(→b)) |
m (Teksterstatting – «/ressurser/eksamen/» til «/res/eksamen/») |
||
| (19 mellomliggende revisjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
| − | = | + | {{EksLenker|1= |
| − | [http://udl.no/matematikk/eksamen-r1-h12 Noen oppgaver løst som videoer fra UDL.no] | + | *[http://udl.no/matematikk/eksamen-r1-h12 Noen oppgaver løst som videoer fra UDL.no] |
| − | + | *[http://ndla.no/nb/node/103948?fag=57933 Løsningsforslag fra NDLA] | |
| + | *[http://www.matematikk.net/res/eksamen/R1/sensur/2012V_Vurderingsskjema_R1.pdf Vurderingsskjema] | ||
| + | *[http://www.matematikk.net/res/eksamen/R1/sensur/2012V_Sensorveiledning_REA3022_MatematikkR1_Varen201.pdf Sensorveiledning] | ||
| + | }} | ||
== DEL EN == | == DEL EN == | ||
| Linje 26: | Linje 29: | ||
==== 1) ==== | ==== 1) ==== | ||
Nullpunkter:<p></p> | Nullpunkter:<p></p> | ||
| − | <math>x^3-3x = \\ x(x^2-3)=\\x(x- \sqrt 3 )(x + \sqrt 3) \\x = - \sqrt3 \quad \vee \quad x = 0 \quad \vee \quad x= \sqrt3</math> | + | <math>x^3-3x = 0\\ x(x^2-3)= 0\\x(x- \sqrt 3 )(x + \sqrt 3) =0 \\x = - \sqrt3 \quad \vee \quad x = 0 \quad \vee \quad x= \sqrt3</math> |
==== 2) ==== | ==== 2) ==== | ||
| Linje 81: | Linje 84: | ||
I B er x = 0 | I B er x = 0 | ||
| − | <math> \frac 2a </math><p></p> | + | <math>y = \frac 2a </math><p></p> |
Koordinater B:<math>(0, \frac 2a)</math> | Koordinater B:<math>(0, \frac 2a)</math> | ||
| Linje 87: | Linje 90: | ||
Arealet av trekanten avgrenset av tangenten og aksene er: | Arealet av trekanten avgrenset av tangenten og aksene er: | ||
<math> A= \frac{2a \cdot \frac 2a}{2} = 2</math><p></p> | <math> A= \frac{2a \cdot \frac 2a}{2} = 2</math><p></p> | ||
| − | Man observerer at arealet er uavhengig av x. | + | Man observerer at arealet er uavhengig av x, eller a om man vil. |
== DEL TO == | == DEL TO == | ||
== Oppgave 4: == | == Oppgave 4: == | ||
| + | |||
| + | ==a)== | ||
| + | |||
| + | Skalarprodukt: | ||
| + | $\vec{AB} \cdot \vec{AC} = |\vec{AB}| \cdot| \vec{AC}| \cdot cos \angle{BAC} \\ | ||
| + | [9,5] \cdot [5,6] = \sqrt{9^2+5^2} \cdot \sqrt{5^2 + 6^2} \cdot cos \angle{BAC} \\ | ||
| + | 45+30 = \sqrt{106} \cdot \sqrt{61} cos \angle{BAC}\\ \angle {BAC} = cos^{-1} ( \frac{75}{\sqrt{6466}}) \\ \angle BAC = 21,1^{\circ}$ | ||
| + | |||
| + | ==b)== | ||
| + | |||
| + | Firkanten ABCD er et parallellogram dersom $\vec{AB} = \vec{DC}.$ D har koordinatene (x,y). Vi får | ||
| + | |||
| + | $[9,5] = [2-x, 4-y] \\ 9=2-x \wedge 5 = 4-y \\ x=-7 \wedge y= - 1 $ | ||
| + | |||
== Oppgave 5: == | == Oppgave 5: == | ||
<math> \vec{AB}=[2,-2]</math><p></p> | <math> \vec{AB}=[2,-2]</math><p></p> | ||
| Linje 108: | Linje 125: | ||
<math>\vec{EF} = [5,-5]</math><p></p>Bruker [1, -1] som rettningsvektor. Parameterfremmstilling:<p></p> | <math>\vec{EF} = [5,-5]</math><p></p>Bruker [1, -1] som rettningsvektor. Parameterfremmstilling:<p></p> | ||
| − | + | $l: \begin{bmatrix} | |
| + | x=2 + t \\ | ||
| + | y=4 - t | ||
| + | \end{bmatrix}$ | ||
=== b) === | === b) === | ||
| Linje 132: | Linje 152: | ||
=== c) === | === c) === | ||
[[Fil:2012-r1-7c.png]] | [[Fil:2012-r1-7c.png]] | ||
| + | |||
| + | Når x = 1,3 er arealet på sitt største, A = 0,85. | ||
== Oppgave 8: == | == Oppgave 8: == | ||
| Linje 173: | Linje 195: | ||
=== b) === | === b) === | ||
| + | |||
| + | Areal av kvadrat er $A= \sqrt{\frac92} \cdot \sqrt{\frac 92} = \frac 92$ | ||
Skravert areale:<p></p> | Skravert areale:<p></p> | ||
| − | <math>\frac 14 \pi r^2 - \frac | + | <math>\frac 14 \pi r^2 - \frac 92 = \frac 94 \pi - \frac{18}{4} = \frac 94(\pi-2)</math> |
== Oppgave 11: == | == Oppgave 11: == | ||
Nåværende revisjon fra 19. okt. 2014 kl. 17:08
DEL EN
Oppgave 1:
a)
1)
<math>f(x) = 5x^3+x-4 \\ f'(x) = 3 \cdot 5x^2 + 1 \\ f'(x) = 15x^2 + 1 </math>
2)
<math>g(x) = 5e^{3x} \\ u = 3x \wedge u' = 3 \\ g'(x) = 5e^u \cdot u' \\ g'(x) = 15e^{3x}</math>
b)
<math> 2\ln(\frac{a^2}{b}) + \ln (a \cdot b) - 3\ln a = \\ 2\ln a^2 - 2\ln b + \ln a + \ln b - 3 \ln a = \\4\ln a - 2\ln b + \ln a + \ln b - 3 \ln a = \\ 2\ln a - \ln b </math>
c)
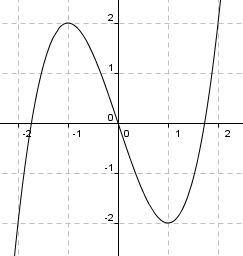
<math> f(x)= x^3-3x</math>
1)
Nullpunkter:
<math>x^3-3x = 0\\ x(x^2-3)= 0\\x(x- \sqrt 3 )(x + \sqrt 3) =0 \\x = - \sqrt3 \quad \vee \quad x = 0 \quad \vee \quad x= \sqrt3</math>
2)
<math>f'(x) = 3x^2-3 \\f'(x) = 0 \\ 3(x^2-1) = 0 \\ x = -1 \quad \vee \quad x = 1 \\ f(-1)= 2 \quad \vee \quad f(1) = -2</math>
Toppunkt (-1,2)
Bunnpunkt (1,-2)
3)
d)
<math>P(x) = x^3-3x^2-x+3 \\ P(3) = 27-27-3+3 =0 \\ \\ P(x):(x-3) \\ (x^3-3x^2-x+3): (x-3) =x^2-1\\-(x^3-3x^2)\\ \quad \quad \quad \quad\quad \quad \quad -(-x+3) \\ \quad \quad \quad \quad\quad \quad \quad \quad\quad \quad \quad\quad \quad \quad 0</math>
Dette gir følgende løsninger:
x = - 1 eller x = 1 eller x = 3.
e)
<math>\vec r(t) = [3,0t ,-4,9t^2] \\ \vec v(t) = \vec r^\prime(t) = [3,0 , -9,8t] \\ \vec a(t) = \vec v^\prime(t) = \vec r^{\prime \prime}(t) = [0 , -9,8] </math>
Oppgave 2:
a)
y = ax + b
a er linjens stigningstall. Dersom man befinner seg et sted på linjen og går en enhetsvektor i x rettning, må man gå a enhetsvektorer i y rettning for å treffe linjen igjen. Rettningsvektor for linjen blir derfor [1,a].
b)
Skalarprodukt:
<math>[1,a_1]\cdot[1,a_2] = 0 \\ 1+ a_1 \cdot a_2 = 0 \\ a_1 \cdot a_2 =-1</math>
c)
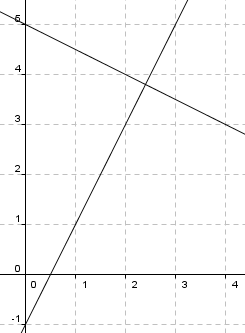
Resultatet i b gir den nye linjen stigningstall minus en halv. b, der linjen skjærer y aksen er fem. Man får da:
<math>y= - \frac 12x+5</math>
d)
Oppgave 3:
a)
<math> f(x)= \frac1x \\ f'(x) = - \frac {1}{x^2} \\ f'(a) = - \frac {1}{a^2} \\ Rett \quad linje: \quad y=ax+b \\ y= - \frac{1}{a^2}x+ b </math>
Finner b ved å bruke punktet (a, f(a)):
<math>y = - \frac{1}{a^2}x+ b \\ \frac 1a = - \frac{1}{a^2}a+ b \\ b= \frac 2a </math>
Som gir likningen
<math>y = - \frac{1}{a^2}x+ \frac 2a</math>
b)
<math>y = - \frac{1}{a^2}x+ \frac 2a</math>
A:
<math> y=0 \\ 0 = - \frac{1}{a^2}x+ \frac 2a \\ \frac{x}{a^2} = \frac 2a \\ x=2a</math>
Koordinater A: (2a,0)
B:
I B er x = 0
<math>y = \frac 2a </math>
Koordinater B:<math>(0, \frac 2a)</math>
c)
Arealet av trekanten avgrenset av tangenten og aksene er:
<math> A= \frac{2a \cdot \frac 2a}{2} = 2</math>
Man observerer at arealet er uavhengig av x, eller a om man vil.
DEL TO
Oppgave 4:
a)
Skalarprodukt: $\vec{AB} \cdot \vec{AC} = |\vec{AB}| \cdot| \vec{AC}| \cdot cos \angle{BAC} \\ [9,5] \cdot [5,6] = \sqrt{9^2+5^2} \cdot \sqrt{5^2 + 6^2} \cdot cos \angle{BAC} \\ 45+30 = \sqrt{106} \cdot \sqrt{61} cos \angle{BAC}\\ \angle {BAC} = cos^{-1} ( \frac{75}{\sqrt{6466}}) \\ \angle BAC = 21,1^{\circ}$
b)
Firkanten ABCD er et parallellogram dersom $\vec{AB} = \vec{DC}.$ D har koordinatene (x,y). Vi får
$[9,5] = [2-x, 4-y] \\ 9=2-x \wedge 5 = 4-y \\ x=-7 \wedge y= - 1 $
Oppgave 5:
<math> \vec{AB}=[2,-2]</math>
Lengde av radius:
<math>r= \frac 12 | \vec{AB}| = \frac 12 \sqrt8 = \sqrt2</math>
Sentrum S, av sirkel: <math>\vec{OS}= \vec{OA} + \frac 12 \vec{AB} = [2,4]+ \frac 12 [2,-2] = [3,3] </math>
Sentrum er i punktet (3,3). Et vilkårlig punkt på sirkelperiferien er (x,y). Vi får:
<math> (x-3)^2 + (y-3)^2 = (\sqrt 2)^2 \\ (x-3)^2 + (y-3)^2 =2 </math>
Oppgave 6:
a)
<math>\vec{EF} = [5,-5]</math>
Bruker [1, -1] som rettningsvektor. Parameterfremmstilling:
$l: \begin{bmatrix} x=2 + t \\ y=4 - t \end{bmatrix}$
b)
Skjæring med x- akse: y = 0 gir t = 4 som gir x = 6. Skjæring i (6,0)
Skjæring med y- akse: x = 0 gir t = -2 som gir y = 6. skjæring i (0, 6)
c)
<math> [2+t-6, 4-t-3] \cdot [1,-1] =0 \\ [t-4, 1-t] \cdot [1,-1] =0 \\ t-4-1+t = 0 \\ t = \frac 52 \\ x = \frac 92 \wedge y = \frac 32</math>
Avstand mello G og l:
<math>\sqrt{( \frac{12}{2}- \frac{9}{2})^2 + (\frac{6}{2}- \frac{3}{2})^2} = \frac{3 \sqrt2}{2}</math>
Oppgave 7:
a)
<math>f(x) = \frac 52 e^{- \frac x2} \\ A = g(x) = \frac{f(x) \cdot x}{2} = \frac {\frac 52 e^{- \frac x2} \cdot x}{2} = \frac 54x e^{- \frac x2}</math>
b)
<math> g'(x)= \frac 54 e^{- \frac x2} + \frac 54 x e^{- \frac x2}\cdot( - \frac 12) = e^{- \frac x2}( \frac 54 - \frac{5x}{8}) \\ g'(x) = 0 \\ x = 2</math>
Inspeksjon viser at g har et maksimum for x=2.
<math>g(2)= \frac{5 \cdot 2}{4} e^{-1} = \frac{5}{2e}</math>
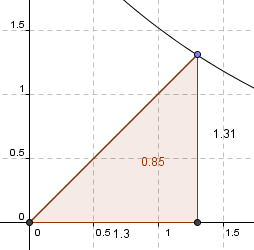
c)
Når x = 1,3 er arealet på sitt største, A = 0,85.
Oppgave 8:
a)
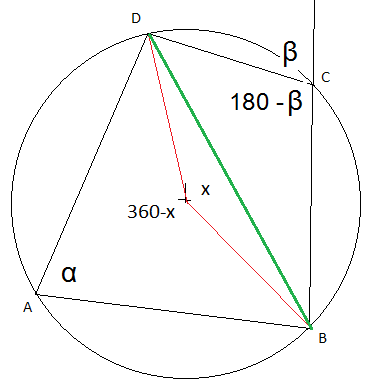
Når en periferivinkel og en sentralvinkel i en sirkel spenner over samme sirkelbue, så er periferivinkelen halvparten så stor som sentralvinkelen. En sentralvinkel har samme gradetall som sirkelbuen den spenner over.
Vinkelen alfa er periferivinkel og spenne over samme bue som sentralvinkelen x. Av det følger:
<math>\alpha = \frac x2</math>
b)
Periferivinkelen 180 grader minus beta, spenner over sirkelbuen DAB. Den sentralvinkel som spenner over samme bue er 360 grader minus x. Fra setningen over får man da:
<math>180^{\circ} - \beta = \frac 12 (360^{\circ} - x)</math>
c)
<math> 180^{\circ} - \beta = \frac 12(360^{\circ} - x) \\ 360^{\circ} - 2 \beta = 360^{\circ} - x \\ x= 2 \beta </math>
Fra a har man at x er lik to alfa, hvilket betyr at alfa er lik beta.
<math>x = 2 \beta \quad \wedge \quad \alpha = \frac x2 \\ 2 \alpha = 2 \beta \\ \alpha = \beta</math>
Oppgave 9:
a)
b)
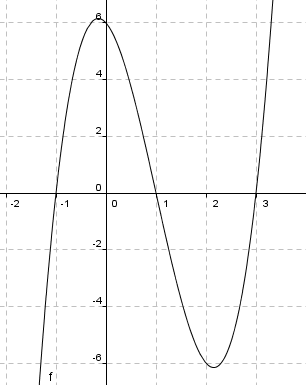
g(x)= 2(x + 2)(x - 1)(x-3)
c)
<math>h(x)= 0,5(x+2)(x-2)(x-2)= 0,5(x+2)(x-2)^2</math>
Oppgave 10:
a)
AC = OB = 3
b)
Areal av kvadrat er $A= \sqrt{\frac92} \cdot \sqrt{\frac 92} = \frac 92$
Skravert areale:
<math>\frac 14 \pi r^2 - \frac 92 = \frac 94 \pi - \frac{18}{4} = \frac 94(\pi-2)</math>
Oppgave 11:
a)
A = det regner
B = det er meldt regn
<math>P(A)= 0,08 \\ P( \overline{A}) = 1-P(A)= 0,92 </math>
b)
<math>P(B|A)=0,90 \\ P(B| \overline{A}) = 0,10 \\P(B) = P(A) \cdot P(B|A) + P( \overline{A}) \cdot P(B| \overline{A}) = 0,08 \cdot 0,90 + 0,92 \cdot 0,10 = 0,164</math>
c)
<math>P( \overline{A}|B) = \frac{P( \overline{A}) \cdot P(B| \overline{A})}{P(B)} = \frac{0,92 \cdot 0,10}{0,164} = 0,56</math>