Spørsmål angående svaret til en integrasjonsoppgave

[Razzy]

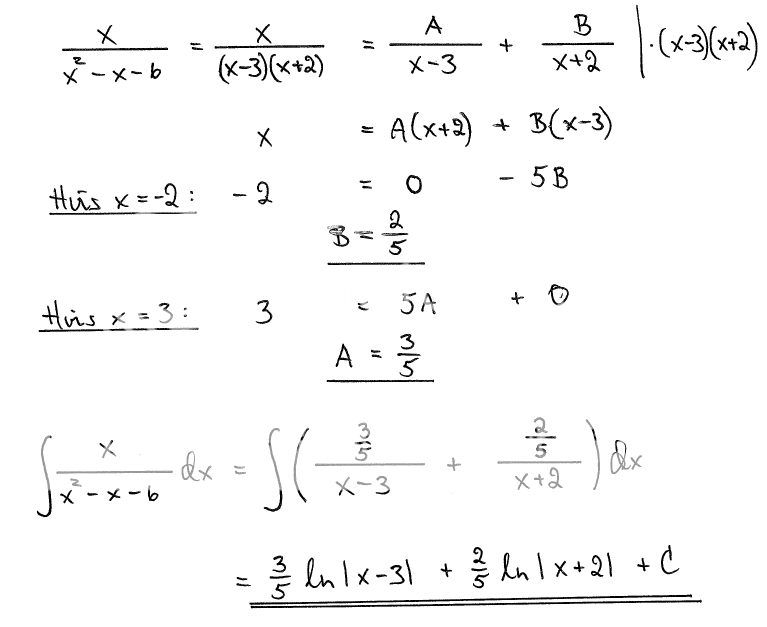
[tex]$$\int {\left( {{{{3 \over 5}} \over {x - 3}} + {{{2 \over 5}} \over {x + 2}}} \right)} dx$$[/tex]

Vi tar en nærmere titt på fasitsvaret. Løser de brudne brøkene og setter konstanten utenfor.

[tex]$$3\int {{1 \over {5\left( {x - 3} \right)}}} dx + 2\int {{1 \over {5\left( {x + 2} \right)}}} dx$$[/tex]

[tex]$$3\int {{1 \over {5x - 15}}} dx + 2\int {{1 \over {5x + 10}}} dx$$[/tex]

[tex]$$3 \cdot {1 \over 5}\ln \left| {5x - 15} \right| + 2 \cdot {1 \over 5}\ln \left| {5x + 10} \right| + C$$[/tex]

[tex]$$\underline {{3 \over 5}\ln \left| {5x - 15} \right| + {2 \over 5}\ln \left| {5x + 10} \right| + C} $$[/tex]

[tex]$${3 \over 5}\ln \left| {5x - 15} \right| + {2 \over 5}\ln \left| {5x + 10} \right| + C \: \ne\: {3 \over 5}\ln \left| {x - 3} \right| + {2 \over 5}\ln \left| {x + 2} \right| + C$$[/tex]

Jeg er ganske sikker på at det ikke er gjort noen matematiske feil her, så hva er grunnen til at uttrykkene får forskjellige verdier når jeg legger dem inn på kalkulatoren?

Det betyr kanskje at man ikke skal selge bjørneskinnet før bjørnen er skut...

[Nebuchadnezzar]

[tex] \frac{3}{5}\ln \left| {5x - 15} \right| + \frac{2}{5}\ln \left| {5x + 10} \right| + C [/tex]

[tex] \frac{3}{5}\ln \left| {5\left( {x - 3} \right)} \right| + \frac{2}{5}\ln \left| {5\left( {x + 2} \right)} \right| + C [/tex]

[tex] \left( {\frac{3}{5}\ln \left| {\left( {x - 3} \right)} \right| + \frac{3}{5}\ln \left( 5 \right)} \right) + \left( {\frac{2}{5}\ln \left| {\left( {x + 2} \right)} \right| + \frac{2}{5}\ln \left( 5 \right)} \right) + C[/tex]

[tex] \frac{3}{5}\ln \left| {x - 3} \right| + \frac{2}{5}\ln \left| {x + 2} \right| + D [/tex]

[tex]\frac{1}{5}\left( {3\ln \left| {x - 3} \right| + 2\ln \left| {x + 2} \right|} \right) + D [/tex]

[Razzy]

[tex] \frac{3}{5}\ln \left| {5x - 15} \right| + \frac{2}{5}\ln \left| {5x + 10} \right| + C [/tex]

[tex] \frac{3}{5}\ln \left| {5\left( {x - 3} \right)} \right| + \frac{2}{5}\ln \left| {5\left( {x + 2} \right)} \right| + C [/tex]

[tex] \left( {\frac{3}{5}\ln \left| {\left( {x - 3} \right)} \right| + \frac{3}{5}\ln \left( 5 \right)} \right) + \left( {\frac{2}{5}\ln \left| {\left( {x + 2} \right)} \right| + \frac{2}{5}\ln \left( 5 \right)} \right) + C[/tex]

[tex] \frac{3}{5}\ln \left| {x - 3} \right| + \frac{2}{5}\ln \left| {x + 2} \right| + D [/tex]

[tex]\frac{1}{5}\left( {3\ln \left| {x - 3} \right| + 2\ln \left| {x + 2} \right|} \right) + D [/tex]

Mellom 3 og 4 linje mister du disse: [tex]$${{3 \over 5}\ln \left( 5 \right)}$$[/tex] og [tex]$${{2 \over 5}\ln \left( 5 \right)}$$[/tex]

Eller vent litt, tviler på Nebuchadnezzar "mister" uttrykk... Hva har du gjort med dem?

Jeg ser du har skiftet ut C til D. Har det noe med saken å gjøre?

[Markonan]

De er alle konstanter, så C + ln-uttrykkene dine = D.
Capicche?

[Razzy]

De er alle konstanter, så C + ln-uttrykkene dine = D.
Capicche?

Capiche: 1940s slang, from It. capisci? "do you understand?" (also coppish, kabish, capeesh, etc.).

Certo, come un pesce! (klart som en fisk)

Takk