Er kanskje litt sløv, men eg brukte utruleg lang tid på å prøve å få til denne oppgåva. Er ikkje sikker på at eg løyser den rett, då den ikkje er behandla i fasiten. Eg er veldig takksam for innspel (ev. om det finst betre måtar å gjere det på)
Oppgåve 1.16
Teikn ein vilkårleg firkant ABCD. Kall midtpunkta på sidene E, F, G og H. Bruk vektorrekning til å vise at firkanten EFGH er eit parallellogram.
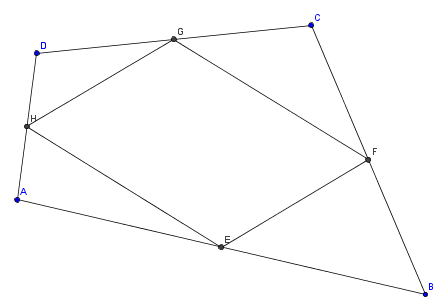
[tex]\vec {HE} = \frac{1}{2}\vec{DA} + \frac{1}{2}\vec{AB}[/tex]
[tex]\vec {HE} = \frac{1}{2}(\vec{DA} + \vec{AB})[/tex]
[tex]\vec {HE} = \frac{1}{2}\vec{DB}[/tex]
[tex]\vec {GF} = \frac{1}{2}\vec{DC} + \frac{1}{2}\vec{CB}[/tex]
[tex]\vec {GF} = \frac{1}{2}(\vec{DC} + \vec{CB})[/tex]
[tex]\vec {GF} = \frac{1}{2}\vec{DB}[/tex]
[tex]\vec {GF} = \vec{HE}[/tex]
Tilsvarande kan ein vise for HG og EF.
Då sidene er parvis parallelle og parvis like lange, er det eit parallellogram, vel?


