
Her er mitt forsøk på løsning:
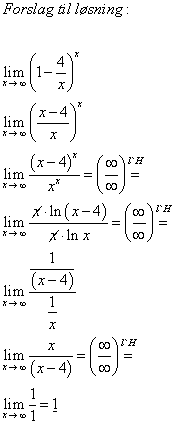
Og hva er så deres kommentar? hehe
Moderators: Aleks855, Gustav, Nebuchadnezzar, Janhaa, DennisChristensen, Emilga

Du deriverer feil 1. gang, tror jeg, men er ikke sikker siden jeg ikke kan se hvilke trinn du har gjortRazzy wrote:Dette er oppgaven slik jeg har fått den:
Her er mitt forsøk på løsning:
Og hva er så deres kommentar? hehe


Hei igjen Nebu, og tusen takk for tilbakemeldingen. Kunne du forklart hva du gjør på linje 3,4 og 5?Nebuchadnezzar wrote:1. [tex]y = \lim_{x \to \infty} \left( 1 - \frac{4}{x} \right)^{x} [/tex]
2. [tex]\ln y = \lim_{x \to \infty} x \ln \left( 1 - \frac{4}{x} \right)[/tex]
3. [tex]n = \frac{1}{x}[/tex]
4. [tex]\ln y = \lim_{n \to 0} \frac{\ln \left( 1 - 4n \right)}{n} \qquad \left[ \frac{0}{0} \right] [/tex]
5. [tex]\ln y = \lim_{n \to 0} \frac{-4}{1-4n}[/tex]
6. [tex]\ln y = -4[/tex]
7. [tex] y = e^{-4}[/tex]

Nabu, dette var gøy! Føles nesten ut som du "leker" litt mer hjernen min her. Men skjønner nå hvordan du har kommet frem til denne utregningen - dette vil jeg teste på mer! Du og alle de knepene dine.Nebuchadnezzar wrote:Liker gjerne å bare skrive regningen uten forklaringer, og la personen jeg hjelper tenke litt selv. Som du har gjort. Flott!
På linje 3 så bytter vi ut [tex]\frac{1}{x}[/tex] med [tex]n[/tex]. Som er et lite knep, slik l`hoptial kan benyttes.
Vi ser at vi har [tex]n=\frac{1}{x}[/tex] vi ser at det at x går mot uendelig så går n mot null. Eventuelt
[tex]\lim_{x \to \infty} [/tex]
[tex] \lim_{\frac{1}{n} \to \infty} [/tex]
[tex] \lim_{n \to 0} [/tex]
Også sjekker jeg bare at den er på riktig form og deriverer ja. Det er kun grensen jeg deriverer. Fordi det er kun den som er en grense. Høyreside har ingenting med venstre side å gjøre, mtp deriveringen.
Men du, prøv å bruke definisjonen av den deriverte til å finne den deriverte av [tex]\ln(x)[/tex]
Da får du bruk for litt av snadderet ovenfor
hehe, du kaller det skitne triks. Men det er morro å kunne noen skitne triks!Aleks855 wrote:Tror Razzy er inne på noe. Nebu er flink i matte fordi han bruker skitne triks og knep!

Nebuchadnezzar wrote:Å være flik i matte kan bety så mye forskjellig
Du er en røver i hoderegning
Du er en kløpper til å regne ut logiske gåter
Du er en maskin når det kommer til bevisføring
Du er kongen når det kommer til algegebra manipulasjon
Eller du bare kan være en rakker til å bruke skitne triks, du har sett før/ kombinere skitne triks til nye skitnere triks.