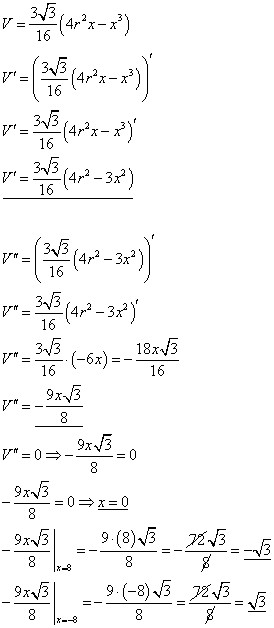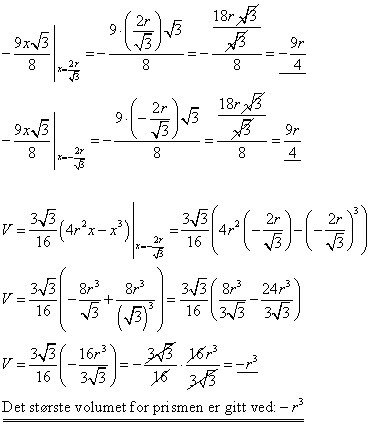Derivasjon - optimalisering

[Vektormannen]

Nå trur jeg du tuller det litt til -- volumet har sin minimale eller maksimale verdi i de punktene der den deriverte er 0. I punktet der den dobbeltderiverte er 0, altså i vendepunktet, har volumet størst forandring. Men det er ikke det du er ute etter. Du vi vil vite når det er størst.

De verdiene for x som er kandidater er altså der den deriverte er 0. Det som gjenstår er som Nebu og mstud foreslo ovenfor: å finne ut hvilke av de to x-verdiene der V'(x) = 0 som er et topp-punkt for volumet. Det kan gjøres på to måter: 1) Du kan lage et fortegnsskjema for den deriverte, eller 2) Du kan finne den dobbeltderiverte (det har du jo allerede gjort nå) og sette inn hver x-verdi og se hvilket fortegn den har. Hvis den dobbeltderiverte er negativ for en x-verdi, krummer grafen nedover. Da må ekstremalpunktet være et topp-punkt. Nå som du allerede har laget et fortegnsskjema for den dobbeltderiverte kan du enkelt se hvilke av de to ekstremalpunktene som er topp-punktet, og da har du funnet den riktige verdien for x som gir størst volum.

Edit: Når det gjelder hvor mange prosent det er snakk om, så er det helt riktig å dele prismevolumet på kulevolumet. Kulevolumet har du allerede (du kan ikke gjøre stort mer med det uttrykket siden du ikke kjenner r) og et uttrykk for volumet av prismet får du når du nå finner x-verdien som gir størst volum.

[mstud]

Tror det har foregått noe korresjon på dette feltet siden sist





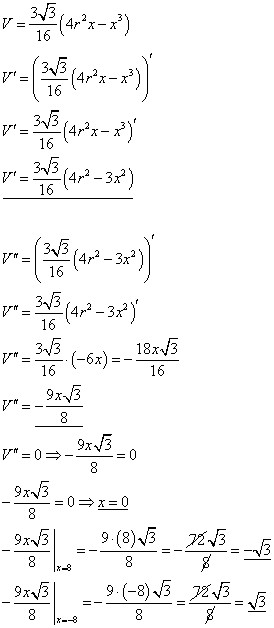
Kan oppgaven løses slik? Det skal stå "punktet" i teksten over fortegnsskjemaet.

Det eneste jeg mangler nå er å sette inn x=0 i volumuttrykket på til å begynne med og se hvilket volum jeg får ut. Dette volumet er da det største denne prisma kan ha.

Nå gjelder det bare å ut: Hvor mange prosent av kulevolumet utgjør prismevolumet i dette tilfelle?

Vel maks prismevolum har jeg akkurat funnet og volumet for en kule er oppgitt. Ok da setter jeg funksjonene lik hverandre, setter inn x=0 og løser? Ai ai captain? Eller "tosk razzy"

[tex]$${V_y} = {V_{kule}}$$[/tex]

[tex]$${{3\sqrt 3 } \over {16}}\left( {4{r^2}x - {x^3}} \right) = {4 \over 3}\pi {r^3}$$[/tex]

nei dette var noe tull, jeg skal finne PROSENT. Da må jeg isåfall dele dele prismevolumet på kulevolumet. Jeg må finne kule volumet.

FØRST:

Det var ikke vendepunkt du skulle finne, men toppunkt. Altså ikke V''=0, men V'=0.
Da får du to verdier for x, du vil vite hvilken som er toppunkt. DETTE KAN DU FINNE UT VED Å:

sette inn de to verdiene av x i V'', den verdien av x som gir negativ V'' er toppunktet. Toppunktet er

ELLER

tegne fortegnsskjema for V'

Du skal ikke få x=0.

Se det du kalte det "fantastiske innlegget" mitt...

[tex](2r-\sqrt {3}x)(2r+\sqrt {3} x)=0[/tex] gir

[tex]2r-\sqrt {3}x=0[/tex] ELLER [tex]2r+\sqrt {3} x=0[/tex]

Dette gir ikke x=0, er du enig ?

[tex]\sqrt {3}x=2r[/tex] ELLER [tex]\sqrt {3}x=-2r[/tex] dvs

[tex]x=\frac {2r}{\sqrt {3}}[/tex] ELLER [tex]x=- \frac {2r}{\sqrt {3}}[/tex]

Så må du finne ut hvilken av disse som er toppunktet (den andre er bunnpunktet.

Sett inn [tex]x=\frac {2r}{\sqrt {3}}[/tex] OG [tex]x=- \frac {2r}{\sqrt {3}}[/tex] i [tex]V^{,,}=-\frac {9x\sqrt {3}}8[/tex]

r er alltid positiv (vi har aldri møtt en negativ radius). Den verdien for x som gir negativt fortegn på V'' er dermed toppunktet, og du har x-verdien ved maksimalt volum, sett denne inn i opprinnelig V, og du har V_{maks}

[Razzy]

Bare så dere får sove i kveld




Enig?? Legger ut prosent-delen.


Tusen takk for hjelpen!

[Vektormannen]

Nesten! Husk at når den dobbeltderiverte er negativ så er ekstremalpunktet et topp-punkt. Du har valgt den som gir positiv dobbeltderivert. Men ellers ser utregningen veldig bra ut (Den eneste forskjellen vil såvidt jeg kan se bli at du får motsatt fortegn på sluttsvaret ditt.)

[Razzy]

Nesten! Husk at når den dobbeltderiverte er negativ så er ekstremalpunktet et topp-punkt. Du har valgt den som gir positiv dobbeltderivert. Men ellers ser utregningen veldig bra ut (Den eneste forskjellen vil såvidt jeg kan se bli at du får motsatt fortegn på sluttsvaret ditt.)

Ah ser hva du sier!

Det er veldig positivt, for jeg merket noe rart når jeg løste resten av oppgaven:



Takk igjen, nå må jeg vel finne loppekassa. Vi snakkes sikkert i morgen! Ha en god natt

[Vektormannen]

Ja, ikke sant , og det gir ikke mye mening med en negativ lengde heller.

Men bra jobbet!