Gauss for å avgjøre bestemt, ubestemt, selvmotsigende

[Aleks855]

Noen av oppgavene i boka mi går ut på å:

"Bruk Gausseliminasjon for å avgjøre om likningssystemene er bestemt, ubestemt eller selvmotsigende"

Jeg gjør det som faller meg inn, men finnes det en lettere måte å avgjøre dette på? Det slår meg at boka skal ha meg til å avgjøre det allerede når matrisen er på trappeform, uten å behøve å regne mer.

Eksempelvis: http://imgur.com/NaA4X

[svinepels]

Hvis koeffisientmatrisen er kvadratisk, kan du jo bare se på determinanten. Som regel raskere enn å bruke Gauss, så det lønner seg dersom man ikke er interessert i selve løsningen.

EDIT: Hvis du får determinant lik 0, vet du fremdeles ikke om det er uendelig mange eller ingen løsninger. Hmm.

[espen180]

Gausseliminasjon er vel den letteste måten, tror jeg.

[Aleks855]

Gausseliminasjon er vel den letteste måten, tror jeg.

Ja, men må man også innom den vanlige "løs likningene"-rutinen? Eller finnes det en lettere måte enn den jeg brukte ovenfor?

[espen180]

Begrepene "bestemt", "ubestemt" og "selvmotsigende" er jo ikke definert for annet enn ligningssystemer. Likevel kan man si noe basert på generelle egenskaper til matrisen. Å bestemme disse egenskapene kan likevel gjøres lettest ved gausseliminasjon. Hva som er lettest kommer som oftest av på hva for informasjon du får oppgitt, og i slike sammenhenger får du som regel an matrise A og en vektor y.

Anta at du har ligningssystemet [tex]Ax=y[/tex], der [tex]x[/tex] og [tex]y[/tex] har samme antall elementer [tex]r[/tex] ([tex]A[/tex] er en kvadratisk matrise). Hvis a har rang [tex]r[/tex], dvs er inverterbar, er systemet alltid bestemt for enhver [tex]y[/tex]. Hvis rangen til [tex]A[/tex] er mindre enn [tex]r[/tex] så vil [tex]y[/tex] være i kolonnerommet til [tex]A[/tex] eller ikke. Hvis den er det, er systemet ubestemt. Hvis ikke, er det selvmotsigende.

[svinepels]

Formulert uten begreper som gjerne dukker opp litt senere i et lineær algebra-kurs:

Dersom man har et ligningssystem [tex]Ax=y[/tex] der A er kvadratisk, så må y kunne skrives som en lineærkombinasjon av kolonnevektorene i A for at systemet skal ha noen løsninger i det hele tatt. Hvis i tillegg det(A)=0, har systemet uendelig mange, men hvis det(A) [symbol:ikke_lik] 0, har systemet nøyaktig én løsning.

Angående det med lineærkombinasjon, så vil det å vise at en slik lineærkombinasjon eksisterer i praksis gå ut på å bruke Gauss-Jordan, men fra et teoretisk synspunkt er det jo interessant.

[Aleks855]

Hva med denne? http://imgur.com/tCwBs

Kan den sies å være selvmotsigende fordi den har en likning som ikke går opp vha. Gauss?

[svinepels]

Ja, det er nettopp slik man oppdager at et ligningssystem er inkonsistent (dvs. har ingen løsninger).

[Aleks855]

Ok, så grafisk sett ville dette betydd at selv om de to andre likningene møtes på et eller annet punkt, så vil den tredje likningen ikke treffe det samme punktet, og ergo er systemet selvmotsigende? Og derfor er de to første likningene uinteressante siden løsningsmengden allerede er Ø?

Det er dette jeg sliter med i matte. Jeg kan løse oppgaver som en sjef, og få karakterer som gjør mamma stolt, men det å FORSTÅ greiene er liksom det som gjør Aleks selv stolt

[svinepels]

Det er umulig for to lineære ligninger i tre variable å "møtes i et punkt". Ser man grafisk på slike ligninger, representerer de uendelig utstrakte plan i rommet, og sett at de har noen punkter til felles, så må disse enten utgjøre en linje (se for deg ikke-parallelle plan krysse hverandre), eller så må planene være identiske og dermed er punktene de har til felles, et helt plan. Klarer du å se dette for deg?

Det er først når vi legger til et tredje plan, at det gir mening å snakke om ett punkt, dvs. nøyaktig én (x,y,z) som de har til felles. Men dersom to av planene er parallelle, uten å sammenfalle, vil systemet uansett ikke ha noen løsninger, og dermed har det siste planet ikke så mye å si. Det var kanskje noe sånt du tenkte.

Det jeg har skrevet i denne posten kan generaliseres til n dimensjoner (men da trenger ikke ting lenger være geometrisk opplagte).

[Aleks855]

Ja, sorry. Mente jo naturligvis plan når det er tre variabler.

Men det jeg mente var at hvis en av likningene ikke går opp (slik som her; 0 = -17), betyr dette da at det ene planet ligger parallelt på et av de andre?

Således, hvis to av likningene er like, altså at de representerer det samme planet, da må det være slik at hvis det finnes løsninger, så må det være en linje, som er den linja der det tredje planet skjærer de to første? Dette vil da være den ubestemte løsningen, altså uendelig mange punkter?

[Nebuchadnezzar]

Stemmer det, men dog gjelder selfølgelig dette bare om du har lineære plan.
Altså ikke noe [tex]x^2[/tex] og [tex]y^2[/tex] eller[tex] z^2[/tex] osv.
Og ja, dette kan bare visualiseres i R2 og R3

Slenger opp noen bilder. Her er eksempler fra R3

En unik løsning





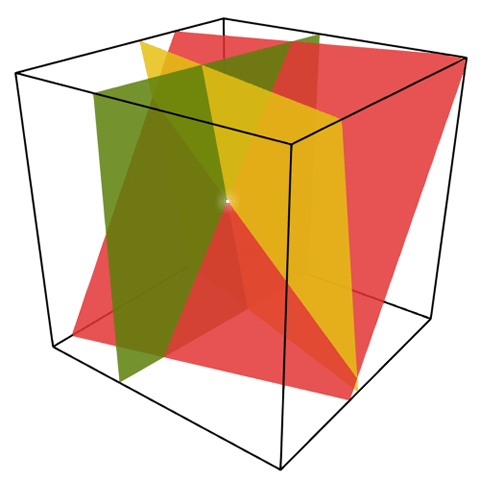
Uendelig mange løsninger




Ingen løsninger

[svinepels]

Hvis to av tre plan er identiske, men det siste ligger parallelt og er ulik de to første, vil det fremdeles ikke være noen løsninger av systemet. Hvis det siste planet ikke er parallelt med de to første, må det krysse dem i en linje som du sier, og løsningen vår blir én-dimensjonal. Men det finnes en tredje mulighet, nemlig at det tredje planet også er identisk med de to andre. Da blir løsningen et helt plan i rommet.

Altså finnes det flere typer uendelige løsningsmengder: linjer, plan , og hele rom når man beveger seg i høyere dimensjoner. Dette diskuteres typisk etter at generelle vektorrom har blitt innført