Integral maraton !

[Determined]

Kjappt og enkelt, men morosamt integral!

$\int \frac{x^2\arctan x}{1+x^2}dx$

[Nebuchadnezzar]

Legg merke til at $x^2/(1+x^2)=(x^2+1-1)/(1+x^2)=1-(1)/(1+x^2)$ så
$\int x^2/(1+x^2)\mathrm{d}x=x-\arctan x+C$. Via delvis integrasjon fås
${\displaystyle \begin{array}{rl}\int \frac{x^2}{1+x^2}\arctan x\mathrm{d}x& =(x-\arctan x)\cdot \arctan x-\int (x-\arctan x)\cdot \frac{1}{1+x^2}\mathrm{d}x\\ & =x\arctan x-{\arctan }^{2}x-[\frac{1}{2}\log (1+x^2)-\frac{1}{2}{\arctan }^{2}x]\\ & =x\arctan x-\frac{1}{2}\arctan x-\frac{1}{2}\log (1+x^2)+\mathcal{C}\end{array}}$

Evnt så er

${\displaystyle \begin{array}{rl}I& =\int \frac{x^2\arctan x+\arctan x-\arctan x}{1+x^2}\mathrm{d}x\\ & =\int \arctan x-\frac{\arctan x}{(\arctan x{)}^{\prime }}\mathrm{d}x\\ & =[x\cdot \arctan x-\int x\left(\frac{1}{1+x^2}\right)\mathrm{d}x]-\frac{1}{2}{\arctan }^{2}x\\ & =x\arctan x-\frac{1}{2}\arctan x-\frac{1}{2}\log (1+x^2)+\mathcal{C}\end{array}}$

via ca like mye arbeid.

Oppgave: En definisjon av logaritmefunksjonen er gitt som følger

${\displaystyle \log x={\int }_1^x\frac{1}{t}\mathrm{d}t}$

Bruk definisjonen ovenfor til å vise at identitetene $\log x^y=y\log x$ og $\log xy=\log x+\log y$ holder.
Her antas det selvsagt at $x$ og $y$ er reelle positive tall.

[Determined]

Oppgave: En definisjon av logaritmefunksjonen er gitt som følger

${\displaystyle \log x={\int }_1^x\frac{1}{t}\mathrm{d}t}$

Bruk definisjonen ovenfor til å vise at identitetene $\log x^y=y\log x$ og $\log xy=\log x+\log y$ holder.
Her antas det selvsagt at $x$ og $y$ er reelle positive tall.

$y\log x=y{\int }_1^x\frac{1}{t}dt={\int }_1^x\frac{y{t}^{y-1}}{t^y}dt=[\log t^y{]}_1^x=\log x^y$

[Nebuchadnezzar]

Tar en diskre bump her

http://folk.ntnu.no/oistes/Diverse/Inte ... eboken.pdf

Har fått arbeidet en del mer på problemene på Del II, og fått
skrevet kanskje 60% ferdig på Del II.

Som vanlig trykker en på selve oppgaveteksten på problemene får en full løsning,
mens trykkes det på tallet får en bare fasitsvaret.

Hva som mangler så langt på Del III er følgende
Konstanter, Catalan's, Apeyrons, Kinkelin osv.
Funksjoner, digamma, polygamma, ${\text{Li}}_2$, Elliptisk
Transformasjoner, Melin, Fourier, Laplace.
Seksjon om kompleks integrasjon, nøkkelhull, og ulike parametriseringer.
Oppgavesammling

[Nebuchadnezzar]

Bestem integralet
${\displaystyle I:={\int }_{\psi }^{\phi }{2}^2(x^2-1)e^{2x}\mathrm{d}x}$
der $\psi$ og $\phi$ er enholdsvis den minste og største løsningen av $x(x-1)=1$.

[Janhaa]

Dette var jo ett lett ubestemte integral ! Svaret var jo artig da...

$I=I_1+I_2=4(\int x^2{e}^{2x}dx-\int e^{2x}dx)$

vha 2 delvis integrasjoner er

$I_1=4e^{2x}(\frac{x^2}{2}+\frac{1}{4}-\frac{x}{2})=e^{2x}(2x^2+1-2x)$
og
$I_1=-2e^{2x}$
slik at

$I=e^{2x}(2x^2-1-2x)+C$

så settes grensene inn, dvs
$\frac{1\pm \sqrt{5}}{2}$
altså:
$I=e(e^{\sqrt{5}}-e^{-\sqrt{5}})=2e\sinh (\sqrt{5})$

[Nebuchadnezzar]

Har som vanlig ei alternativ løsning.. Noe i samme gate som omegaoppgaven.
${\displaystyle {\int }_{\psi }^{\phi }{2}^2(x^2-1)e^{2x}\mathrm{d}x=[(2\cdot \stackrel{1}{\overbrace{x(x-1)}}-1)\cdot e^{2x}{]}_{\psi }^{\phi }=[e^{2x}{]}_{\psi }^{\phi }=e^{2\phi }-e^{2\psi }.}$
For å slippe den delvise integrasjonen så kan en bruke følgende ansatz*
${\displaystyle \int (x^2-1)\cdot e^{2x}\mathrm{d}x=(A{x}^2+Bx+C)\cdot e^{2x}+\mathcal{C}.}$
Der derivasjon av likningen
${\displaystyle (x^2-1)\cdot e^{2x}=[2A\cdot x^2+2(A+B)\cdot x+(2C+B)]\cdot e^{2x},}$
lar oss bestemme konstantene $A$, $B$ og $C$, ved å sammenlikne koeffisienter.
=======================================================
*Kommer fra om vi deriverer $P\cdot e^x$ fås $G\cdot e^x$, der $G$ og $P$ er
polynomer av samme grad. ($G=P+P^{\prime }$.)

Artig oppgave ja =)

[Nebuchadnezzar]

Har da enda en luring på lager! Gitt $R>r>0$ vis at

$f(\theta )=\frac{1}{2\pi }\frac{R^2-r^2}{R^2-2Rr\cos \theta +r^2},$

er normert for $\theta \in [0,2\pi ]$. Altså
${\int }_0^{2\pi }f(\theta )\mathrm{d}\theta =1$
$f(\theta )$ kalles ofte for Poisson Kernel og er mye brukt i harmonisk analyse.
http://en.wikipedia.org/wiki/Poisson_kernel
Merk det er kulere om en løser integralet uten bruk av komplekse størrelser :p

[Nebuchadnezzar]

Her er et nytt integral:

${\int }_0^{\frac{\pi }{2}}\frac{1}{1+(\tan x{)}^{\sqrt{2}}}dx$

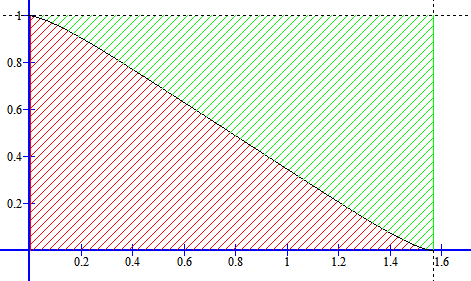
$${\int }_0^{\pi /2}\frac{\mathrm{d}x}{1+\tan (x{)}^{\sqrt{2}}}=\frac{1}{2}\left(\frac{\pi }{2}\right)=\frac{\pi }{4}$$

[Janhaa]

Her er et nytt integral:

${\int }_0^{\frac{\pi }{2}}\frac{1}{1+(\tan x{)}^{\sqrt{2}}}dx$

$${\int }_0^{\pi /2}\frac{\mathrm{d}x}{1+\tan (x{)}^{\sqrt{2}}}=\frac{1}{2}\left(\frac{\pi }{2}\right)=\frac{\pi }{4}$$

http://mathforum.org/library/drmath/view/63680.html

[Nebuchadnezzar]

Bildet er løsningen på oppgaven, siden det røde og grønne området er like stort =)
Dermed er integralet halvparten av et rektangel med høyde $1$ og bredde $\pi /2$.
Så løsningen for noen dager siden, og syntes den var latterlig pen.

[Nebuchadnezzar]

Tar en diskre dobbelpost her, alle tre kan løses med samme fremgangsmåte.

$\begin{array}{rl}{I}_A& ={\int }_0^{\pi /2}\frac{\cos x}{\sin x+\cos x}\mathrm{d}x\\ I_B& ={\int }_0^{\pi }x(\cos x{)}^4\mathrm{d}x\\ I_C& ={\int }_0^{\pi /2}\log \left(\frac{(1+\sin x{)}^{1+\cos x}}{1+\cos x}\right)\mathrm{d}x\end{array}$

Det anbefales å bruke $x\mapsto a-b-u$. Merk at dette ikke nødvendigvis gjør hele jobben =)

[Janhaa]

Tar en diskre dobbelpost her, alle tre kan løses med samme fremgangsmåte.
$\begin{array}{rl}{I}_A& ={\int }_0^{\pi /2}\frac{\cos x}{\sin x+\cos x}\mathrm{d}x\end{array}$

god gammal integrasjonsoppgave (ubestemt);

$I=\frac{1}{2}\int \frac{2\cos (x)}{\sin (x)+\cos (x)}dx=\frac{1}{2}\int \frac{(\cos (x)+\sin (x))+(\cos (x)-\sin (x))}{\sin (x)+\cos (x)}dx$


$I=\frac{1}{2}\int dx+\frac{1}{2}\int \frac{\cos (x)-\sin (x)}{\sin (x)+\cos (x)}dx=\frac{1}{2}x+\frac{1}{2}\int \frac{du}{u}=\frac{1}{2}x+\frac{1}{2}\ln |u|=\frac{1}{2}x+\frac{1}{2}\ln |\cos (x)+\sin (x)|+C$

innsatt grenser gir

$I=\frac{\pi }{4}$

[Janhaa]

Tar en diskre dobbelpost her, alle tre kan løses med samme fremgangsmåte.
$\begin{array}{rl}{I}_B& ={\int }_0^{\pi }x(\cos x{)}^4\mathrm{d}x\end{array}$
Det anbefales å bruke $x\mapsto a-b-u$. Merk at dette ikke nødvendigvis gjør hele jobben =)

kan løses med tabulator integrasjon, sjøl om det er traktor-jobb, fikk da:
$I_B=\frac{3{\pi }^2}{16}$

sikkert lettere måte...

[Nebuchadnezzar]

Tja du kan jo prøve å bruke at

${\int }_0^{a}f(x)\mathrm{d}x={\int }_0^{a}f(a-x)\mathrm{d}x$

Da kan du få et uttrykk med bare ${\cos }^{4}x$, og
deretter kan en vel bruke sin favorittmetode. Betafunksjonen
eller Wallis integralene, eller tabular..