Problem med regnestykke

[Kake med tau]

Wolfram Alpha får at [tex]\frac{2\pi i}{1-e^{\frac{2\pi i}{3}}}=\frac{2 \pi}{\sqrt{3}}[/tex] (https://www.wolframalpha.com/input/?i=2 ... %2F3%29%29)

Hvordan får de til det? [tex]1-e^{\frac{2\pi i}{3}}[/tex] er ikke rent imaginært!

[Gustav]

Hos meg gir ikke wolfram et rent reellt tall når jeg følger linken din. Svaret er $i π-π/\sqrt(3)$

[Kake med tau]

Under "Alternate Forms":

[Gustav]

Under "Alternate Forms":

$(-1)^{\frac23}$ er ikke et reellt tall. Det er komplekst med både reell og imaginær del.

EDIT: en måte å se det på er at $-1=e^{\pi i}$, så $(-1)^{\frac23}=e^{\frac{2\pi i}{3}}=\cos \frac{2\pi}{3}+i\sin \frac{2\pi}{3}$

[Kake med tau]

[tex](-1)^{\frac{2}{3}}=((-1)^{\frac{1}{3}})^2=(-1)^2=1[/tex], eller [tex](-1)^{\frac{2}{3}}=((-1)^2)^{\frac{1}{3}}=(1)^{\frac{1}{3}}=1[/tex], er ikke det riktig?

[Gustav]

[tex](-1)^{\frac{2}{3}}=((-1)^{\frac{1}{3}})^2=(-1)^2=1[/tex], eller [tex](-1)^{\frac{2}{3}}=((-1)^2)^{\frac{1}{3}}=(1)^{\frac{1}{3}}=1[/tex], er ikke det riktig?

Dessverre ikke riktig når man jobber i det komplekse plan.

[Kake med tau]

Ok, men hvis [tex]e^{(\pi+2\pi k)i}=-1[/tex], så vil [tex](-1)^{\frac{2}{3}}=e^{(\frac{2\pi}{3}+\frac{4\pi k}{3})i}[/tex], for k=1 blir [tex]e^{(\frac{2\pi}{3}+\frac{4\pi}{3})i}=e^{2\pi i}=1[/tex], er dette feil?

[Gustav]

Ok, men hvis [tex]e^{(\pi+2\pi k)i}=-1[/tex], så vil [tex](-1)^{\frac{2}{3}}=e^{(\frac{2\pi}{3}+\frac{4\pi k}{3})i}[/tex], for k=1 blir [tex]e^{(\frac{2\pi}{3}+\frac{4\pi}{3})i}=e^{2\pi i}=1[/tex], er dette feil?

Nei, det er ikke feil. Og det er strengt tatt ikke feil at $(-1)^{\frac23}=1$ heller. Problemet er at uttrykket $(-1)^{\frac23}$ har tre mulige komplekse verdier (som svarer til k=0,1,2 i det du skriver over). Og funksjonen $f(z)=z^{\frac23}$ er (rettere sagt kan betraktes som) en multifunksjon. (når vi betrakter f som en kompleks funksjon)

Det som wolfram mener i svaret du linket til er principalverdien til $(-1)^{\frac23}$, og den svarer til k=0 i uttrykket ditt over.

[Kake med tau]

Ok, tusen takk for hjelpen!

Grunnen til at jeg lurer på dette er fordi jeg skulle regne ut et integral ved å bruke residues. Jeg endte opp med: (r skal bli til x)
[tex](1-e^{\frac{2\pi i}{3}})\int_{0}^{\infty} \frac{r^\frac{1}{3}}{(r+a)(r+b)}=\frac{a^{1/3}-b^{1/3}}{a-b}2\pi i[/tex], fasiten sier at hele integralet skal være [tex]\frac{a^{1/3}-b^{1/3}}{a-b}\frac{2\pi}{\sqrt{3}}[/tex]

Dette funker bare (antar at jeg ikke har gjort noen feil tidligere i stykket) hvis [tex]\frac{2\pi i}{1-e^{\frac{2\pi i}{3}}}=\frac{2\pi}{\sqrt{3}}[/tex]

[Gustav]

Dette funker bare (antar at jeg ikke har gjort noen feil tidligere i stykket) hvis [tex]\frac{2\pi i}{1-e^{\frac{2\pi i}{3}}}=\frac{2\pi}{\sqrt{3}}[/tex]

Dette stemmer nok ikke.

Sikker på at det ikke skal være absoluttverdien [tex]|\frac{2\pi i}{1-e^{\frac{2\pi i}{3}}}|=\frac{2\pi}{\sqrt{3}}[/tex] ?

[Kake med tau]

Jeg er ikke sikker, nei. (Absoluttverdi blir hvertfall ikke nevnt i eksemplene jeg har sett på; "Integration along a branch cut") Jeg må gjøre om [tex]\int_{0}^{\infty} \frac{r^\frac{1}{3}}{(r+a)(r+b)}[/tex] til [tex]\int_{0}^{\infty} \frac{x^\frac{1}{3}}{(x+a)(x+b)}[/tex]. Kan jeg gjøre om det første integralet til det andre ved å ta absoluttverdien? [tex]r=\sqrt{x^2+y^2}[/tex], så hvis [tex]y=0[/tex] er det kanskje greit?

[Gustav]

Hvor går grenkuttet? (branch cut) Og hvor kommer faktoren $1-e^{\frac{2\pi i}{3}}$ foran integralet fra?

[Kake med tau]

Funksjonen er [tex]f(z)=\frac{z^{1/3}}{(z+a)(z+b)}=\frac{e^{\frac{1}{3}log z}}{(z+a)(z+b)}[/tex], [tex]|z|>0, 0<arg(z)<2\pi[/tex], grenkuttet er vel da mellom [tex]0[/tex] og [tex]2\pi[/tex]. Jeg bruker stien som på figuren:

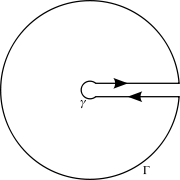
Radien til den minste sirkelen er [tex]\rho[/tex], og radien til den største er [tex]R[/tex].

Har at [tex]\int_{\rho}^R f(r) dr + \int_{\Gamma} f(r) dr + \int_{R}^{\rho} f(r) dr + \int_{\gamma} f(r) dr = 2\pi i(Res_{z=-a} f(z) + Res_{z=-b} f(z))[/tex], viser at
[tex]\int_{\Gamma} f(r) dr[/tex] og [tex]\int_{\gamma} f(r) dr[/tex] begge går mot [tex]0[/tex], når henholdsvis [tex]R[/tex] og [tex]\rho[/tex] går mot [tex]\infty[/tex] og [tex]0[/tex]

Da:

[tex]\int_{0}^{\infty} \frac{r^{1/3}}{(r+a)(r+b)}-\int_{0}^{\infty} \frac{r^{1/3}e^{\frac{2\pi i}{3}}}{(z+a)(z+b)} dr=2\pi i(\frac{a^{1/3}-b^{1/3}}{a-b})[/tex], [tex]a>b>0[/tex], har brukt at i det første integralet er [tex]z=re^{0 i}[/tex], og i det andre [tex]z=re^{2\pi i}[/tex]
[tex](1-e^{\frac{2\pi i}{3}})\int_{0}^{\infty}\frac{r^{1/3}}{(r+a)(r+b)}dr=2\pi i(\frac{a^{1/3}-b^{1/3}}{a-b})[/tex]