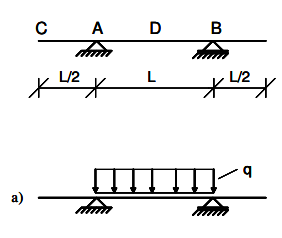
Antar at opplageret i punkt B er et glidelager siden jeg ikke kan huske at vi drev på med statisk ubestemte systemer i mek1

Vertikal opplagerkraft i A og B må nødvendigvis være [tex]F_A = F_B = \frac{qL}{2}[/tex]. Lag et snitt mellom punkt A (x = 0) og punkt B, momentlikevekt om snittet vil da være gitt ved (med strekk i underkant av bjelken):
[tex]M(x) = \frac{qL}{2}x-\frac{qx^2}{2} = \frac{qLx}{2}\left(1-\frac{x}{L}\right)[/tex]
Bjelken differensialligning: [tex]M(x) = -EI\frac{\mathrm{d}^2w}{\mathrm{d}x^2}[/tex], hvor [tex]w[/tex] er nedbøyning.
Integrerer én gang. Får:
[tex]\frac{\mathrm{d}w}{\mathrm{d}x} = -\frac{q}{2EI}\left(\frac{1}{2}Lx^2-\frac{x^3}{3}\right) + C[/tex]
Nok en integrasjon:
[tex]w(x) = -\frac{q}{2EI}\left(\frac{1}{6}Lx^3-\frac{x^4}{12}\right)+Cx+D[/tex]
To randbetingelser: [tex]w(0) = w(L) = 0[/tex]
[tex]w(0) = D = 0[/tex]
[tex]w(L) = -\frac{q}{2EI}\left(\frac{L^4}{6}-\frac{L^4}{12}\right)+CL = 0 \ \Rightarrow \ C = \frac{q}{2EI}\cdot\frac{L^3}{12}[/tex]
Og vi får:
[tex]w(x) = -\frac{qLx^3}{12EI}\left(1-\frac{1}{2}\frac{x}{L}\right)+\frac{qL^3x}{24EI} = -\frac{qLx^3}{12EI}\left[1-\frac{1}{2}\left(\frac{x}{L}\right)-\frac{1}{2}\left(\frac{L}{x}\right)^2\right][/tex]
Merk at dette uttrykket kun gjelder mellom punkt A og punkt B. Siden du har to leddlager kan det ikke overføres moment til bjelkeutstikkene. Det du derimot vet er at vinkelen som dannes mellom den nedbøyde bjelken og den opprinnelige posisjonen (en vannrett linje) må være lik på begge sider av opplager A (og B forsåvidt). Vinkelen [tex]\theta[/tex] i punkt A (x=0) er gitt som:
[tex]\theta = \left.\frac{\mathrm{d}w}{\mathrm{d}x}\right|_{x=0} = \left.-\frac{3qLx^2}{12EI}+\frac{2qx^3}{12EI}+\frac{qL^3}{24EI}\right|_{x=0} = \frac{qL^3}{24EI}[/tex]
Her er det også rimelig å anta at vinkelen er liten, altså kan man bruke approksimasjonen av sinus for små vinkler: [tex]\sin{\theta} \approx \theta[/tex]
Du får da at nedbøyningen i punkt C er gitt som: [tex]u = \theta \cdot \frac{L}{2} = \frac{qL^4}{48EI}[/tex]