$A_{sirkel} = \pi (\frac 12 a)^2 = \frac 14 \pi a^2$
Areal av svart område:
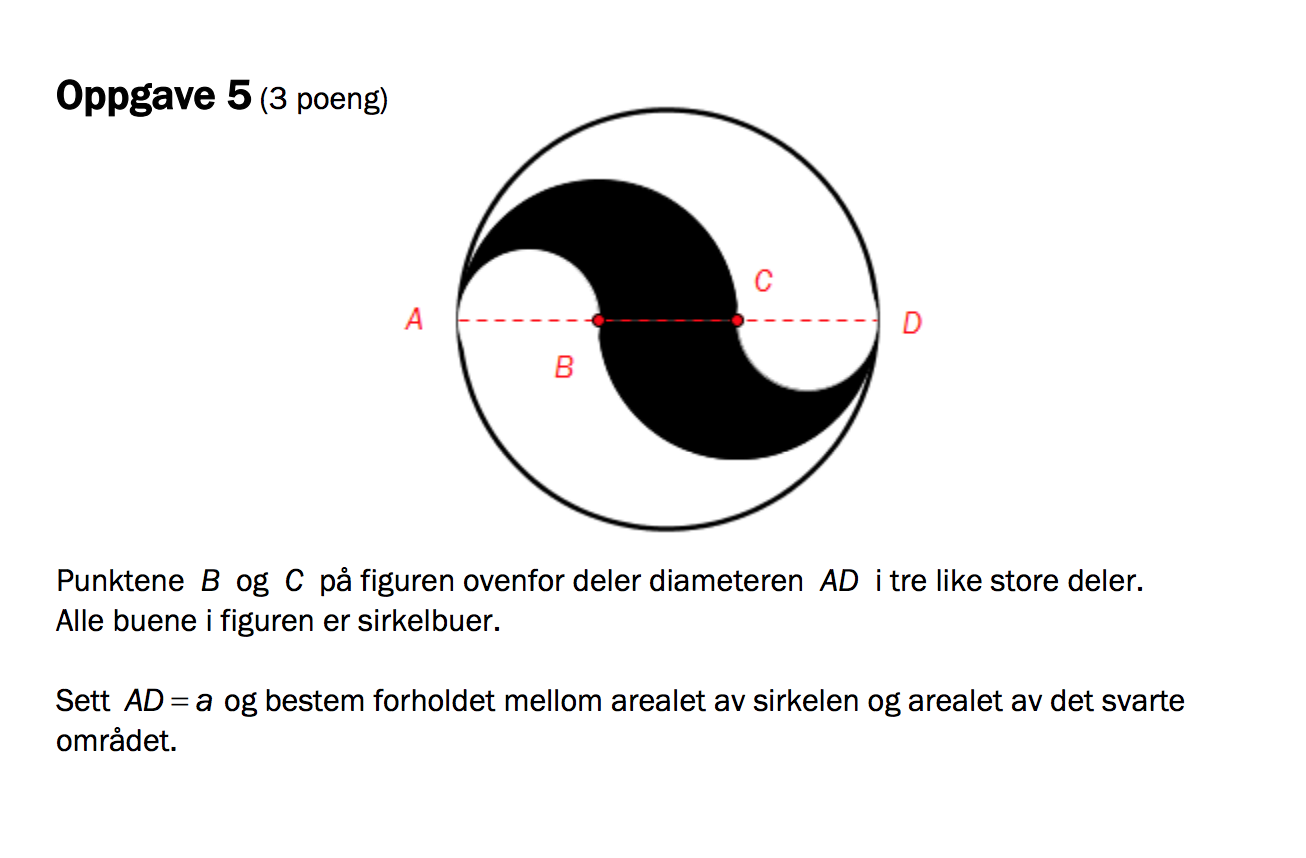
Om du flipper den nederste delen til andre siden, vil du se at man får en svart sirkel med diameter AC, som har en hvit sirkel med diameter AB inni seg. Arealet av det svarte området blir da $\pi(\frac 12 AC)^2 - \pi(\frac 12 AB)^2$ Får opplyst at diameteren består av tre like store deler, så siden $AD = \frac 33a$, så er $AC = \frac 23 a$ og $AB = \frac 13 a$ Setter dette inn i uttrykket:
$ A_{svart} = \pi(\frac 12 \frac 23 a)^2 - \pi(\frac 12 \frac 13 a)^2 = \pi(\frac 13 a)^2 - \pi(\frac 16 a)^2 = \pi \frac 19 a^2 - \pi \frac {1}{36} a^2 = \pi(\frac {4 - 1}{36}a^2 = \pi \frac {3}{36}a^2 = \pi \frac {1}{12}a^2$
Forhold: $\frac {A_{svart}}{A_{sirkel}} = \frac { \frac {1}{12}}{ \frac 14 } = \frac {4}{12} = \frac 13 = 33$ %




