Oppgave
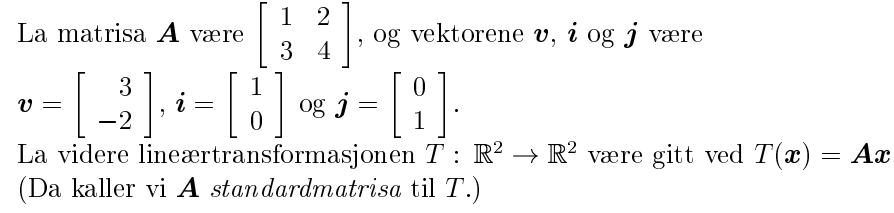

Løsning
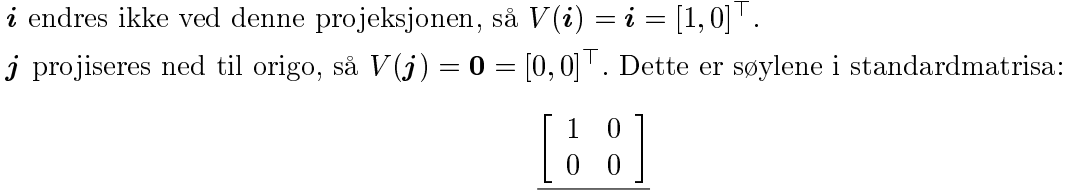
Moderators: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa
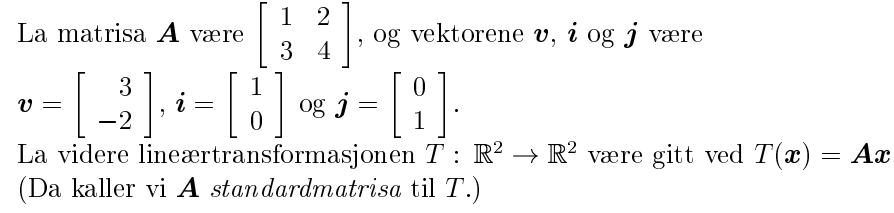

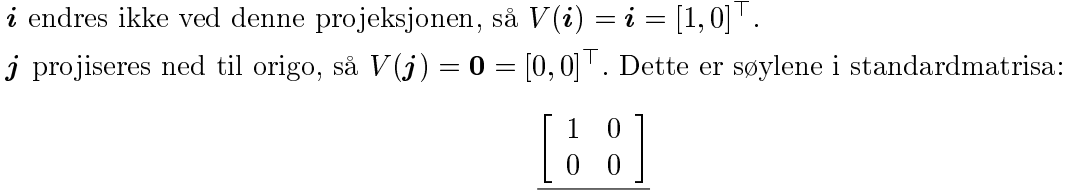

Vi er gitt at $V: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ er projeksjon vinkelrett på $x$-aksen. Det vil si at for alle vektorer $\begin{pmatrix} x \\ y \end{pmatrix} \in \mathbb{R}^2$ har vi at $$V\left(\begin{pmatrix} x \\ y \end{pmatrix}\right) = \begin{pmatrix} x \\ 0 \end{pmatrix},$$ så $$V(\textbf{i}) = \begin{pmatrix} 1 \\ 0 \end{pmatrix};$$ $$V(\textbf{j}) = \begin{pmatrix} 0 \\ 0 \end{pmatrix}.$$linematrise wrote:Trenger hjelp med å forstå spørsmålet, og hvordan man går frem for å løse en slik oppgave. Forstår ikke hva "V(i)", kan ikke se noen steder hvor "V" er definert.
Oppgave
Løsning
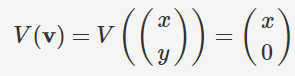

$V$ er en funksjon som sender vektorer i $\mathbb{R}^2$ til vektorer i $\mathbb{R}^2$.hmmm wrote:Jeg har vanskelig for å forstå dette. Hvorfor blander du inn v? Altså V(v), hvor kommer den inn? Ser den er nevnt i innledningen i oppgaven, men ser ikke den nevnt. Standarmatrisen får du ved å sette sammen i og j, korrekt?
Det her skjønner jeg ikke:
Hva foregår egentlig her? Hva tilsier at V(v) er V(x/y) som igjen er (x/0)?