Geometri

[Guest]

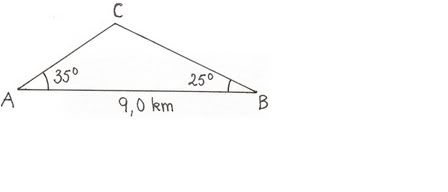
Figuren viser et trekantet område ABC, der AB = 9,0 km, CAB = 35° og ABC = 25°.



c) M er midtpunktet på AC. Finn lengden av BM. (fasit:BM = 8,3 km)
d) Et punkt D ligger på AC. Finn lengden av AD når BD = 2AD. (fasit: AD = 3,3 km)


På

[Solar Plexsus]

c) Her er vinkel C = 180[sup]o[/sup] - 25[sup]o[/sup] - 35[sup]o[/sup] = 120[sup]o[/sup]. Vha. av sinussetningen får vi at

AC/sin25[sup]o[/sup] = AB/sin120[sup]o[/sup]

AC = 9*sin25[sup]o[/sup]/([symbol:rot]3/2) = 6[symbol:rot]3*sin25[sup]o[/sup]

AM = AC/2 = 3[symbol:rot]3*sin25[sup]o[/sup].

Nå gir cosinussetningen at

BM[sup]2[/sup]
= AB[sup]2[/sup] + AM[sup]2[/sup] - 2*AB*AM*cos35[sup]o[/sup]
= 9[sup]2[/sup] + (3[symbol:rot]3*sin25[sup]o[/sup])[sup]2[/sup] - 2*9*3[symbol:rot]3*sin25[sup]o[/sup]*cos35[sup]o[/sup].
= 81 + 27*sin[sup]2[/sup]25[sup]o[/sup] - 54[symbol:rot]3*sin25[sup]o[/sup]*cos35[sup]o[/sup]

som gir BM [symbol:tilnaermet] 7,3 km.


d) Ifølge cosinussetningen er

BD[sup]2[/sup] = AB[sup]2[/sup] + AD[sup]2[/sup] - 2*AB*AD*cos35[sup]o[/sup]

(2AD)[sup]2[/sup] = 9[sup]2[/sup] + AD[sup]2[/sup] - 2*9*cos35[sup]o[/sup]*AD.

3AD[sup]2[/sup] + 18*cos35[sup]o[/sup]*AD - 81 = 0

AD = (-18*cos35[sup]o[/sup] [symbol:plussminus] [symbol:rot] d) / (2*3)

der

d = (18*cos35[sup]o[/sup])[sup]2[/sup] - 4*3*(-81) = 324*cos[sup]2[/sup]35[sup]o[/sup] + 972 = 18[sup]2[/sup](3 + cos[sup]2[/sup]35[sup]o[/sup]).

I.o.m. at AD > 0, blir

AD = 3*[-cos35[sup]o[/sup] + kv.rot(3 + cos[sup]2[/sup]35[sup]o[/sup])]

AD [symbol:tilnaermet] 3,3 (km).

[Guest]

Takk