Regresjon, ax^2+bx+c

[fbhdif]

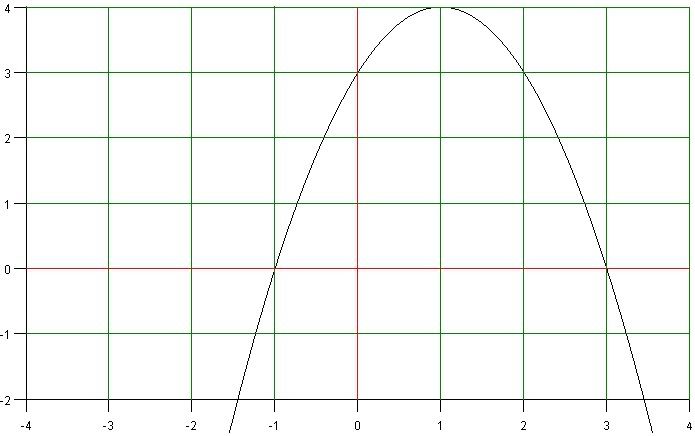
Har en annengradsfunksjonm, eller rettere sagt en derivert tredjegradsfunksjon, men det er uvesentlig.

Jeg har funnet ut at funksjonsuttrykket er [tex]f(x)=-x^2+2x+3[/tex] ved å prøve og feile.
Vet at jeg har en funksjon på kalkulatoren, Quadreg, som klarer dette, men hvordan kan jeg regne det ut for hånd?

Altså, hvordan finner jeg funksjonen til en parabel?

[*Sorcerer*]

f(x) kan faktoriseres som [tex]f(x) = a(x-x_1)(x-x_2)[/tex]
der x1 og x2 er nullpunktene til f(x)

Hvis a er negativ vender grafen den hule siden ned (konkav), og hvis a er positiv vender grafen den hule siden opp (konveks).

[fbhdif]

f(x) kan faktoriseres som [tex]f(x) = a(x-x_1)(x-x_2)[/tex]
der x1 og x2 er nullpunktene til f(x)

Hvis a er negativ vender grafen den hule siden ned (konkav), og hvis a er positiv vender grafen den hule siden opp (konveks).

Flott, takk skal du ha!
Hva er a'en?

Hvis jeg har f(x) = -ax^2 ..., vil jeg ha -a(x-x1)(x-x2) ?

[*Sorcerer*]

a'en er den samme a'en som i [tex]f(x) = ax^2 + bx + c = 0[/tex]
Så du kan velge den selv. Den bare ganger opp uttrykket.

[fbhdif]

Stemmer det, tenkte ikke på at det var en definisjon og ikke et konkret eksempel.. heh