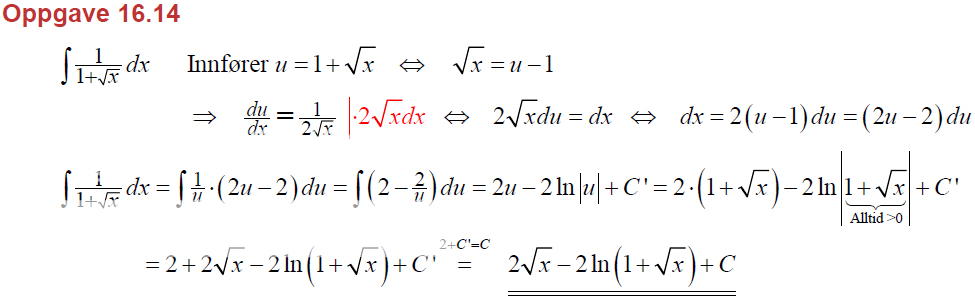Ubestemt integral - unknown

[Razzy]

Til Razzy.

Var derfor jeg nevnte dette eksempelet, slik at du fikk benyttet både variabel skifte og delvis integrasjon.

Skal hjelpe deg litt mer på vei:

[tex]\int \frac{1}{1+sqrt{x}} \ dx[/tex]

[tex]u=1+sqrt{x}[/tex]

[tex]du=\frac{1}{2 \cdot \sqrt{x}} dx[/tex]

[tex]\int \frac {1}{u}\cdot \frac{2\cdot \sqrt{x}}{2\cdot sqrt{x}} dx[/tex]

[tex]\int \frac{1}{u}\cdot 2\cdot sqrt{x}\ du[/tex]

Så hvis [tex]u=1+sqrt{x} \Rightarrow \sqrt{x}=u-1[/tex].....

Jeg visste jeg hadde sett dette uttrykket før, til og med læreren min slet med det!



Kjempeflott, nå ha jeg noe å fundere på!

[Razzy]

Du trenger kun å bruke variabelskifte.

[tex]\int \frac{ e^{\sqrt{x}}}{\sqrt{x}}dx [/tex]

[tex]u=sqrt{x}[/tex]

[tex]du=\frac{1}{2 \cdot \sqrt{x}}dx[/tex]

[tex]\int \frac{e^{u}}{\sqrt{x}} dx \Rightarrow \int {e^{u}\cdot \frac{2}{2\cdot sqrt{x}} dx[/tex]

[tex]\int {e^{u}\cdot 2 du=2\cdot e^{u}+C=2\cdot e^{\sqrt{x}}+C[/tex]

Syntes det var lettere å forstå hvis man:

[tex]\int \frac{ e^{\sqrt{x}}}{\sqrt{x}}dx [/tex]

[tex]u=sqrt{x}[/tex]

[tex]$$du = {1 \over {2\cdot\sqrt x }}dx \Rightarrow dx = 2\sqrt x $$[/tex]

[tex]$$\int {{{{e^u}} \over u}} 2 \cdot u \cdot du$$[/tex] (vi har skiftet alt av [tex]$${\sqrt x }$$[/tex] til u)

[tex]$$\int {2{e^u}} du$$[/tex]...

Men man har altså lov til å kun skifte ut det man selv ønsker? Tiltross for at vi har samme uttrykk i funksjonen? Slik du gjorde her: [tex]$$\int {{{{e^u}} \over {\sqrt x }}} dx$$[/tex]

[Andreas345]

Ja, det var bare for å gjenkjenne "du"-en jeg hadde definert. Men kan jo selvfølgelig gjøre det på din måte og.

[mstud]

Du trenger kun å bruke variabelskifte.

[tex]\int \frac{ e^{\sqrt{x}}}{\sqrt{x}}dx [/tex]

[tex]u=sqrt{x}[/tex]

[tex]du=\frac{1}{2 \cdot \sqrt{x}}dx[/tex]

[tex]\int \frac{e^{u}}{\sqrt{x}} dx \Rightarrow \int {e^{u}\cdot \frac{2}{2\cdot sqrt{x}} dx[/tex]

[tex]\int {e^{u}\cdot 2 du=2\cdot e^{u}+C=2\cdot e^{\sqrt{x}}+C[/tex]

Syntes det var lettere å forstå hvis man:

[tex]\int \frac{ e^{\sqrt{x}}}{\sqrt{x}}dx [/tex]

[tex]u=sqrt{x}[/tex]

[tex]$$du = {1 \over {2\cdot\sqrt x }}dx \Rightarrow dx = 2\sqrt x $$[/tex]

[tex]$$\int {{{{e^u}} \over u}} 2 \cdot u \cdot du$$[/tex] (vi har skiftet alt av [tex]$${\sqrt x }$$[/tex] til u)

[tex]$$\int {2{e^u}} du$$[/tex]...

Men man har altså lov til å kun skifte ut det man selv ønsker? Tiltross for at vi har samme uttrykk i funksjonen? Slik du gjorde her: [tex]$$\int {{{{e^u}} \over {\sqrt x }}} dx$$[/tex]

Hvor mange ganger en skriver den substituerte som u, velger man selv, og men enkelte ganger kan den ene av skrivemåtene være en fordel, men som oftest er det bare en smakssak

[mstud]

Ja, det har du uansett, for alt som står bak det integraltegnet er på et vis ganget med to når du har et uttrykk på formen {2*v*w}

Av og til må man bare få ting på plass i hodet ett hundre ganger før det sitter

[tex]$$\left( {2 \cdot x \cdot {e^x}} \right) \Leftrightarrow 2\left( {x \cdot {e^x}} \right) \Leftrightarrow \cancel {\left( {2x \cdot 2{e^x}} \right)?$$[/tex]

[tex]$$\left( {2 \cdot x \cdot {e^x}} \right) \ne 2\left( {x \cdot {e^x}} \right)}?$$[/tex]Disse to siste her er faktisk like, men hvis det hadde stått 2(x+e^x), hadde du måttet gange både x og e^x med 2 hver for seg, slik du ville gjøre med gangestykket her!

Saken er altså:
[tex]\left( {2 \cdot x \cdot {e^x}} \right) \Leftrightarrow 2\left( {x \cdot {e^x}} \right) \Leftrightarrow \cancel {\left( {2x \cdot 2{e^x}} \right)} [/tex] , men [tex]\left( {2 \cdot x \cdot {e^x}} \right) = 2\left( {x \cdot {e^x}} \right)=2x \dot e^x[/tex]


Kan også vise at [tex]{\left( {2x \cdot 2{e^x}} \right)=4x \cdot e^x}[/tex]
Du ser forskjellen hvis jeg illustrerer med tall: 2(1*1)=2*1*1=2, og dette er feil: 2(1*1)=2*1*2*1=2*2=4, det samme gjelder altså for 2(x*e^x)


men jeg så plutselig nå at det så ut som jeg hadde svart ja til alt dette, men det var altså ikke det jeg svarte ja på ...

[Razzy]

Til Razzy.

Var derfor jeg nevnte dette eksempelet, slik at du fikk benyttet både variabel skifte og delvis integrasjon.

Skal hjelpe deg litt mer på vei:

[tex]\int \frac{1}{1+sqrt{x}} \ dx[/tex]

[tex]u=1+sqrt{x}[/tex]

[tex]du=\frac{1}{2 \cdot \sqrt{x}} dx[/tex]

[tex]\int \frac {1}{u}\cdot \frac{2\cdot \sqrt{x}}{2\cdot sqrt{x}} dx[/tex]

[tex]\int \frac{1}{u}\cdot 2\cdot sqrt{x}\ du[/tex]

Så hvis [tex]u=1+sqrt{x} \Rightarrow \sqrt{x}=u-1[/tex].....

[tex]\int \frac{1}{1+sqrt{x}} \ dx[/tex]

[tex]u=1+sqrt{x}[/tex]

[tex]du=\frac{1}{2 \cdot \sqrt{x}} dx[/tex]

[tex]$$dx = 2\sqrt x \cdot du$$[/tex]

[tex]\int \frac{1}{u}\cdot 2\cdot sqrt{x}\ du[/tex]

Så hvis [tex]u=1+sqrt{x} \Rightarrow \sqrt{x}=u-1[/tex]

[tex]$$\int {{1 \over u}} 2\left( {u - 1} \right)\;du$$[/tex]

[tex]$$\int {{1 \over u}} \left( {2u - 2} \right)\;du$$[/tex]

[tex]$$\int {\left( {u - {2 \over u}} \right)\;du} $$[/tex]

[tex]2u - 2\ln \left| u \right| + C^\prime[/tex]

Herfra er det bare å følge eksempelet nedenfor...



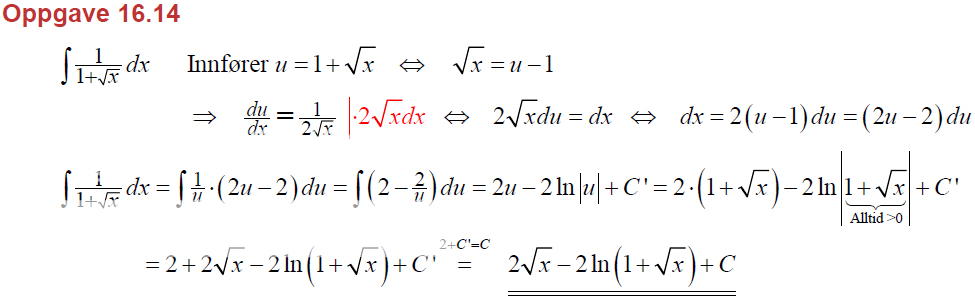
Håper ikke jeg får så vanskelige oppgaver på eksamen, tror denne er en av få som er så vanskelige.

Men en ting stusser jeg på:

Var derfor jeg nevnte dette eksempelet, slik at du fikk benyttet både variabel skifte og delvis integrasjon.

Det er ikke brukt delvis integrasjon på uttrykket ovenfor, kun substitusjon?

[mstud]

Så du innlegget mitt over? JEG drukner hele tiden her

[Razzy]

Ja, det har du uansett, for alt som står bak det integraltegnet er på et vis ganget med to når du har et uttrykk på formen {2*v*w}

Av og til må man bare få ting på plass i hodet ett hundre ganger før det sitter

[tex]$$\left( {2 \cdot x \cdot {e^x}} \right) \Leftrightarrow 2\left( {x \cdot {e^x}} \right) \Leftrightarrow \cancel {\left( {2x \cdot 2{e^x}} \right)?$$[/tex]

[tex]$$\left( {2 \cdot x \cdot {e^x}} \right) \ne 2\left( {x \cdot {e^x}} \right)}?$$[/tex]Disse to siste her er faktisk like, men hvis det hadde stått 2(x+e^x), hadde du måttet gange både x og e^x med 2 hver for seg, slik du ville gjøre med gangestykket her!

Saken er altså:
[tex]\left( {2 \cdot x \cdot {e^x}} \right) \Leftrightarrow 2\left( {x \cdot {e^x}} \right) \Leftrightarrow \cancel {\left( {2x \cdot 2{e^x}} \right)} [/tex] , men [tex]\left( {2 \cdot x \cdot {e^x}} \right) = 2\left( {x \cdot {e^x}} \right)=2x \dot e^x[/tex]


Kan også vise at [tex]{\left( {2x \cdot 2{e^x}} \right)=4x \cdot e^x}[/tex]
Du ser forskjellen hvis jeg illustrerer med tall: 2(1*1)=2*1*1=2, og dette er feil: 2(1*1)=2*1*2*1=2*2=4, det samme gjelder altså for 2(x*e^x)


men jeg så plutselig nå at det så ut som jeg hadde svart ja til alt dette, men det var altså ikke det jeg svarte ja på ...

Jeg skjønner det, jeg skjønner det!! Jippi!!

[Andreas345]

Ja, ser det nå. De hadde skrevet om utrykket litt, så man slapp det.

[Razzy]

Ja, ser det nå. De hadde skrevet om utrykket litt, så man slapp det.

Flott, da har vi orden i sysakene.

Har du hatt R2? Du er jo mildt sagt ganske dreven i integrasjon.

Det jeg har lært nå, er at delvis integrasjonsmetode og brøk oppspaltningsmetode brukes kun når substitusjon ikke fungerer!

[mstud]

Ja, ser det nå. De hadde skrevet om utrykket litt, så man slapp det.

Flott, da har vi orden i sysakene.

Har du hatt R2? Du er jo mildt sagt ganske dreven i integrasjon.

Det jeg har lært nå, er at delvis integrasjonsmetode og brøk oppspaltningsmetode brukes kun når substitusjon ikke fungerer!

Eller evt. i skrivesakene

Mener å ha sett at Andreas345 har hatt noen matematikkfag @ UiB i signaturlinjen sin tidligere, og i så fall bør han vel være dreven i integrasjon, sånn som jeg kanskje skal bli et vakkert år 2012 f.eks.


Hva bruker du hvis ingen av delene fungerer?

Svar: ten.kkitametam

Svaret står baklengs, slik det forhåpentligvis ikke gjør i matematikkboken

[Razzy]

Eller evt. i skrivesakene

Mener å ha sett at Andreas345 har hatt noen matematikkfag @ UiB i signaturlinjen sin tidligere, og i så fall bør han vel være dreven i integrasjon, sånn som jeg kanskje skal bli et vakkert år 2012 f.eks.


Hva bruker du hvis ingen av delene fungerer?

Svar: ten.kkitametam

Svaret står baklengs, slik det forhåpentligvis ikke gjør i matematikkboken

Da har man evt brukt veldig mye unødvendig tid på en prøve, hvis man ikke får det til ved noen av de metodene Hvis ingen av dem fungerer... Da begynner man på nytt!