Delvis integrasjon
Posted: 20/02-2011 18:34


Jeg ser du setter 2/3 utenfor integraltegnet, og det kan du gjøre fordi det er et konstantledd og trenger dermed ikke være endel av ALLE faktorer innenfor?Janhaa wrote:det i rødt blir;
[tex](2/3)\int x^{3/2}*x^{-1}\,dx=(2/3)\int x^{1/2}\,dx=(4/9)x^{2/3} [/tex]
Matematikk er nok bare hobby nå.Razzy wrote:Jeg ser du setter 2/3 utenfor integraltegnet, og det kan du gjøre fordi det er et konstantledd og trenger dermed ikke være endel av ALLE faktorer innenfor?Janhaa wrote:det i rødt blir;
[tex](2/3)\int x^{3/2}*x^{-1}\,dx=(2/3)\int x^{1/2}\,dx=(4/9)x^{2/3} [/tex]
Deretter ser jeg du har brukt potensregel når det gjelder potens gange potens..
Takk Janhaa, ikke for å grave, men har du studert matte lenge? For her går det kjapt!
Googlet kjemiker, så avansert men spennende ut. Det er nok antagligvis for komplisert for meg, men får se, man skal aldri si aldriJanhaa wrote:Matematikk er nok bare hobby nå.
Har studert matte ca 2 år full tid på høyskole/universitet (er kjemiker).
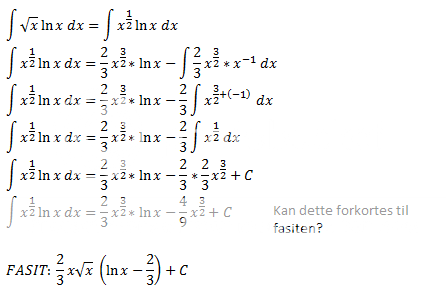
Ok. 2/3*x + 4, her kunne jeg trukket 4 utenfor?Fibonacci92 wrote:Razzy!
2/3 må være faktor i alle LEDD, men du har bare et ledd siden det bare er gangetegn/deletegn. Hadde det stått pluss eller minus mellom noen av tallene som f.eks. 2/3*x + 4 kan du ikke trekke 2/3 utenfor...
Jeg gjorde dette allerede på linje nr 3, mener jeg hvertfall...Fibonacci92 wrote: Står det derimot 2/3*x*e^x kan du trekke 2/3 utenfor, siden det bare er gangetegn mellom hvert konstant og variabel.
Fantastisk, skal forsøke å gjøre dette med min utregning, må bare sette meg helt inn i det herNebuchadnezzar wrote:Ser riktig ut dette ( i mine øyne )
Trekk [tex]\frac{2}{3}[/tex] utenfor og skriv [tex]x^{\frac{2}{3}}[/tex] som [tex]x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}[/tex]
siden [tex]x^a \cdot x^b = x^{a+b} [/tex]
Jeg er enig i alt du gjør teknisk, og at man kan skrive det slik. Nå gjenstår det bare for meg å sette meg inn i det, så skal jeg poste svar senere idag (har akkurat stått opp)Nebuchadnezzar wrote:[tex]\frac{2}{3}x+4=\frac{2}{3}(x+6)[/tex]
og [tex]\frac{4}{9}=\frac{2}{3}\cdot\frac{2}{3}[/tex]
[tex]\frac{2}{3}x+\frac{4}{9}=\frac{2}{3}x+\frac{2}{3}\cdot\frac{2}{3}=\frac{2}{3}(x+\frac{2}{3})[/tex]
Hei og god morgenNebuchadnezzar wrote:Ikke noe problem
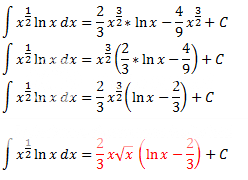
Dette ser bra ut vet du.Nebuchadnezzar wrote:Ser da riktig ut dette, om du lurer på om det er riktig så bare gang inn i parentesen igjen. Da ser du om det ligner.
[tex]x^{\frac{3}{2}}=x^{\frac{1}{2}+\frac{2}{2}}=x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}=\sqrt{x}\cdot{x^{\frac{1}{1}}=x\sqrt{x}[/tex]
