
Delvis integrasjon
Moderators: Aleks855, Gustav, Nebuchadnezzar, Janhaa, DennisChristensen, Emilga
det i rødt blir;
[tex](2/3)\int x^{3/2}*x^{-1}\,dx=(2/3)\int x^{1/2}\,dx=(4/9)x^{2/3} [/tex]
[tex](2/3)\int x^{3/2}*x^{-1}\,dx=(2/3)\int x^{1/2}\,dx=(4/9)x^{2/3} [/tex]
La verken mennesker eller hendelser ta livsmotet fra deg.
Marie Curie, kjemiker og fysiker.
[tex]\large\dot \rho = -\frac{i}{\hbar}[H,\rho][/tex]
Marie Curie, kjemiker og fysiker.
[tex]\large\dot \rho = -\frac{i}{\hbar}[H,\rho][/tex]
Jeg ser du setter 2/3 utenfor integraltegnet, og det kan du gjøre fordi det er et konstantledd og trenger dermed ikke være endel av ALLE faktorer innenfor?Janhaa wrote:det i rødt blir;
[tex](2/3)\int x^{3/2}*x^{-1}\,dx=(2/3)\int x^{1/2}\,dx=(4/9)x^{2/3} [/tex]
Deretter ser jeg du har brukt potensregel når det gjelder potens gange potens..
Takk Janhaa, ikke for å grave, men har du studert matte lenge? For her går det kjapt!
Bygg.ing @ Hib - 2 året.
Matematikk er nok bare hobby nå.Razzy wrote:Jeg ser du setter 2/3 utenfor integraltegnet, og det kan du gjøre fordi det er et konstantledd og trenger dermed ikke være endel av ALLE faktorer innenfor?Janhaa wrote:det i rødt blir;
[tex](2/3)\int x^{3/2}*x^{-1}\,dx=(2/3)\int x^{1/2}\,dx=(4/9)x^{2/3} [/tex]
Deretter ser jeg du har brukt potensregel når det gjelder potens gange potens..
Takk Janhaa, ikke for å grave, men har du studert matte lenge? For her går det kjapt!
Har studert matte ca 2 år full tid på høyskole/universitet (er kjemiker).
La verken mennesker eller hendelser ta livsmotet fra deg.
Marie Curie, kjemiker og fysiker.
[tex]\large\dot \rho = -\frac{i}{\hbar}[H,\rho][/tex]
Marie Curie, kjemiker og fysiker.
[tex]\large\dot \rho = -\frac{i}{\hbar}[H,\rho][/tex]
Googlet kjemiker, så avansert men spennende ut. Det er nok antagligvis for komplisert for meg, men får se, man skal aldri si aldriJanhaa wrote:Matematikk er nok bare hobby nå.
Har studert matte ca 2 år full tid på høyskole/universitet (er kjemiker).
Er jeg forresten i mål når det gjelder likningen, eller har jeg snublet over en feil?
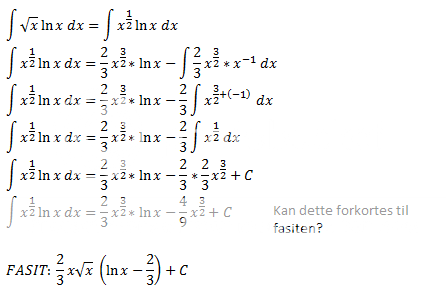
Bygg.ing @ Hib - 2 året.
-
Nebuchadnezzar
- Fibonacci

- Posts: 5648
- Joined: 24/05-2009 14:16
- Location: NTNU
Ser riktig ut dette ( i mine øyne )
Trekk [tex]\frac{2}{3}[/tex] utenfor og skriv [tex]x^{\frac{2}{3}}[/tex] som [tex]x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}[/tex]
siden [tex]x^a \cdot x^b = x^{a+b} [/tex]
Trekk [tex]\frac{2}{3}[/tex] utenfor og skriv [tex]x^{\frac{2}{3}}[/tex] som [tex]x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}[/tex]
siden [tex]x^a \cdot x^b = x^{a+b} [/tex]
"Å vite hva man ikke vet er og en slags allvitenhet" - Piet Hein
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
-
Fibonacci92
- Abel

- Posts: 665
- Joined: 27/01-2007 22:55
Razzy!
2/3 må være faktor i alle LEDD, men du har bare et ledd siden det bare er gangetegn/deletegn. Hadde det stått pluss eller minus mellom noen av tallene som f.eks. 2/3*x + 4 kan du ikke trekke 2/3 utenfor...
Står det derimot 2/3*x*e^x kan du trekke 2/3 utenfor, siden det bare er gangetegn mellom hvert konstant og variabel.
2/3 må være faktor i alle LEDD, men du har bare et ledd siden det bare er gangetegn/deletegn. Hadde det stått pluss eller minus mellom noen av tallene som f.eks. 2/3*x + 4 kan du ikke trekke 2/3 utenfor...
Står det derimot 2/3*x*e^x kan du trekke 2/3 utenfor, siden det bare er gangetegn mellom hvert konstant og variabel.
-
Nebuchadnezzar
- Fibonacci

- Posts: 5648
- Joined: 24/05-2009 14:16
- Location: NTNU
[tex]\frac{2}{3}x+4=\frac{2}{3}(x+6)[/tex]

og [tex]\frac{4}{9}=\frac{2}{3}\cdot\frac{2}{3}[/tex]
[tex]\frac{2}{3}x+\frac{4}{9}=\frac{2}{3}x+\frac{2}{3}\cdot\frac{2}{3}=\frac{2}{3}(x+\frac{2}{3})[/tex]
og [tex]\frac{4}{9}=\frac{2}{3}\cdot\frac{2}{3}[/tex]
[tex]\frac{2}{3}x+\frac{4}{9}=\frac{2}{3}x+\frac{2}{3}\cdot\frac{2}{3}=\frac{2}{3}(x+\frac{2}{3})[/tex]
"Å vite hva man ikke vet er og en slags allvitenhet" - Piet Hein
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
Ok. 2/3*x + 4, her kunne jeg trukket 4 utenfor?Fibonacci92 wrote:Razzy!
2/3 må være faktor i alle LEDD, men du har bare et ledd siden det bare er gangetegn/deletegn. Hadde det stått pluss eller minus mellom noen av tallene som f.eks. 2/3*x + 4 kan du ikke trekke 2/3 utenfor...
Jeg gjorde dette allerede på linje nr 3, mener jeg hvertfall...Fibonacci92 wrote: Står det derimot 2/3*x*e^x kan du trekke 2/3 utenfor, siden det bare er gangetegn mellom hvert konstant og variabel.
Uansett takk forsvar
Bygg.ing @ Hib - 2 året.
Fantastisk, skal forsøke å gjøre dette med min utregning, må bare sette meg helt inn i det herNebuchadnezzar wrote:Ser riktig ut dette ( i mine øyne )
Trekk [tex]\frac{2}{3}[/tex] utenfor og skriv [tex]x^{\frac{2}{3}}[/tex] som [tex]x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}[/tex]
siden [tex]x^a \cdot x^b = x^{a+b} [/tex]
Jeg er enig i alt du gjør teknisk, og at man kan skrive det slik. Nå gjenstår det bare for meg å sette meg inn i det, så skal jeg poste svar senere idag (har akkurat stått opp)Nebuchadnezzar wrote:[tex]\frac{2}{3}x+4=\frac{2}{3}(x+6)[/tex]
og [tex]\frac{4}{9}=\frac{2}{3}\cdot\frac{2}{3}[/tex]
[tex]\frac{2}{3}x+\frac{4}{9}=\frac{2}{3}x+\frac{2}{3}\cdot\frac{2}{3}=\frac{2}{3}(x+\frac{2}{3})[/tex]
Uansett takk for svar Nebuchadnezzar du er alltid våken, hehe
Bygg.ing @ Hib - 2 året.
-
Nebuchadnezzar
- Fibonacci

- Posts: 5648
- Joined: 24/05-2009 14:16
- Location: NTNU
Ikke noe problem
"Å vite hva man ikke vet er og en slags allvitenhet" - Piet Hein
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
Hei og god morgenNebuchadnezzar wrote:Ikke noe problem
Ser meg rett og slett blind på det du skrev tidligere, skjønner hva du sier, men visste ikke hvor jeg skulle bruke det i ligningen min?
Resultatet ble:
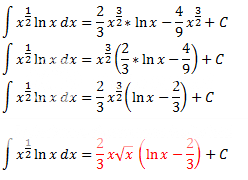
Bygg.ing @ Hib - 2 året.
-
Nebuchadnezzar
- Fibonacci

- Posts: 5648
- Joined: 24/05-2009 14:16
- Location: NTNU
Ser da riktig ut dette, om du lurer på om det er riktig så bare gang inn i parentesen igjen. Da ser du om det ligner.
[tex]x^{\frac{3}{2}}=x^{\frac{1}{2}+\frac{2}{2}}=x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}=\sqrt{x}\cdot{x^{\frac{1}{1}}=x\sqrt{x}[/tex]
[tex]x^{\frac{3}{2}}=x^{\frac{1}{2}+\frac{2}{2}}=x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}=\sqrt{x}\cdot{x^{\frac{1}{1}}=x\sqrt{x}[/tex]
"Å vite hva man ikke vet er og en slags allvitenhet" - Piet Hein
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
Dette ser bra ut vet du.Nebuchadnezzar wrote:Ser da riktig ut dette, om du lurer på om det er riktig så bare gang inn i parentesen igjen. Da ser du om det ligner.
[tex]x^{\frac{3}{2}}=x^{\frac{1}{2}+\frac{2}{2}}=x^{\frac{1}{2}}\cdot x^{\frac{2}{2}}=\sqrt{x}\cdot{x^{\frac{1}{1}}=x\sqrt{x}[/tex]

Bygg.ing @ Hib - 2 året.

