Jeg startet med å velge (gjette) strømretningene
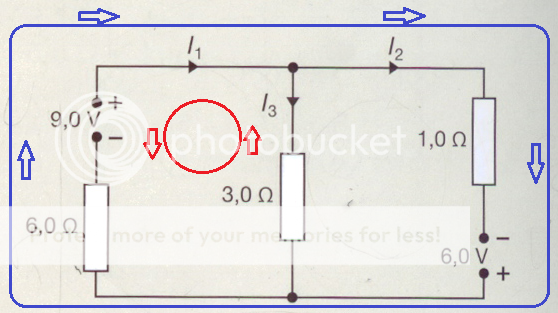 Utregning:
Utregning:
Kirschoffs første lov sier:
[tex]$${l_1} = {l_2} + {l_3}$$[/tex]
Kirschoffs andre lov sier:
1. [tex]$$9,0v + 6,0v = 6,0\Omega *{l_1} + 1,0\Omega *{l_2}$$[/tex]
2. [tex]$$ - 9,0v = - 6,0\Omega *{l_1} - 3,0\Omega *{l_3}$$[/tex]
_________________________________
Vi omskriver den første likningen ved å bruke kirschoffs første lov:
[tex]$$9,0v + 6,0v = 6,0\Omega *\left( {{l_2} + {l_3}} \right) + 1,0\Omega *{l_2}$$[/tex]
[tex]$$9,0v + 6,0v = 6,0\Omega *{l_2} + 6,0\Omega *{l_3} + 1,0\Omega *{l_2}$$[/tex]
[tex]$$9,0v + 6,0v = 7,0\Omega *{l_2} + 6,0\Omega *{l_3}$$[/tex]
_________________________________
Vi omskriver den andre likningen ved å bruke kirschoffs første lov:
[tex]$$ - 9,0v = - 6,0\Omega *\left( {{l_2} + {l_3}} \right) - 3,0\Omega *{l_3}$$[/tex]
[tex]$$ - 9,0v = - 6,0\Omega *{l_2} - 6,0\Omega *{l_3} - 3,0\Omega *{l_3}$$[/tex]
[tex]$$9,0v = 6,0\Omega *{l_2} + 9,0\Omega *{l_3}$$[/tex] (her trakk jeg sammen og ganget med -1)
_________________________________
1. [tex]$$7,0\Omega *{l_2} + 6,0\Omega *{l_3} = 15v$$[/tex]
2. [tex]$$6,0\Omega *{l_2} + 9,0\Omega *{l_3} = 9v$$[/tex]
Kalkulatoren løser disse likningene med to ukjente for oss (vi kan også gjøre dette med regning, ved å bruke innsettingsmetoden)
[tex]$$3,0A \wedge - 1,0A$$[/tex]
Grunnen til at vi får svaret [tex]$$ - 1,0A$$[/tex] er at strømmen i virkeligheten går omvendt retning av hva vi regnet med.




