matematikk.net

Hei, har kommet til en oppgave jeg har litt problemer med. Kan dere fortelle meg hva dere gjør i praksis når dere skal løse en slik oppgave?

Dette tenker jeg, og å sette opp ligningene er det jeg har mest trøbbel med.

1. Sett opp Kirschoffs 1. lov
2. Velg strømretninger (2 stk, enten venstre/høyre lomme eller hele kretsen)
3. Sett opp to ligninger (NB: husk riktige fortegn)
4. Løs ligningene ved hjelp av ligningen jeg satt opp på punkt 1.
5. Tolk svarene, hvis negative svar, så er strømretningen valgt feil et sted.




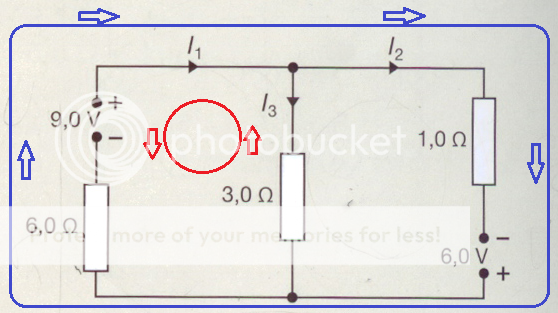
Her er et eksempel fra læreboken

Jeg kan vise deg hvordan jeg ville løst den.

Som i oppskriften din begynner du med å sette opp at det skal gå like mye strøm inn som ut av knutepunktet øverst (dette er Kirchoffs 1. lov.) Da får du den første av tre ligninger: [tex]I_1 = I_2 + I_3[/tex].

Så må du bruke Kirchoffs 2. lov for å finne to ligninger til. Kirchoffs 2. lov dreier seg om hvordan spenningen varierer rundt en strømsløyfe. Vi tenker oss at vi følger en ladd partikkel rundt én runde. Da må den ende opp på et sted med samme potensial, altså må totalt spenningsfall være 0.

Vi kan kalle strømsløyfene for henholdsvis 1 (til venstre) og 2 (til høyre).
Velger et startpunkt i sløyfe 1, f.eks. ved knutepunktet vi så på over her. Så bestemmer vi oss for en retning vi vil gå gjennom sløyfen i. Det er akkurat det samme hvilken retning som velges, så lenge vi er klar på to regler: Når vi kommer til en mostand og går gjennom denne i samme retning som den oppsatte strømretningen, skal den resulterende spenningen ha positivt fortegn. Når vi går gjennom en motstand i motsatt retning av oppsatt strømretning, skal spenningen ha negativt fortegn. Den andre regelen er at spenningen over en spenningskilde er positiv når vi går gjennom kilden fra minuspol til plusspol, og negativ hvis vi går gjennom den motsatt vei.

Vi kan f.eks. ta i retning med klokka. Så begynner vi å gå gjennom sløyfen. Da er det viktig å huske på de fortegnskonvensjonene nevnt ovenfor. Vi går gjennom motstanden i samme retning som oppsatt strømretning, så vi får spenningen [tex]I_3 \cdot 3[/tex] (positivt fortegn.) Så går vi videre og kommer til motstanden på 6 ohm. Nå går vi også i samme retning som strømmen [tex]I_1[/tex], og får da spenningen [tex]I_1 \cdot 6[/tex]. Så kommer vi til batteriet og går fra minuspol til plusspol. Det gir også en positiv spenning på 9V. Det Kirchoffs 2. lov er at summen av de spenningene vi har funnet, skal bli 0. Det gir oss andre ligning:

[tex]3I_3 + 6I_1 + 9 = 0[/tex]

Kan du klare å finne den siste ligningen selv?

Jeg startet med å velge (gjette) strømretningene




Utregning:

Kirschoffs første lov sier:

[tex]$${l_1} = {l_2} + {l_3}$$[/tex]

Kirschoffs andre lov sier:

1. [tex]$$9,0v + 6,0v = 6,0\Omega *{l_1} + 1,0\Omega *{l_2}$$[/tex]

2. [tex]$$ - 9,0v = - 6,0\Omega *{l_1} - 3,0\Omega *{l_3}$$[/tex]
_________________________________


Vi omskriver den første likningen ved å bruke kirschoffs første lov:

[tex]$$9,0v + 6,0v = 6,0\Omega *\left( {{l_2} + {l_3}} \right) + 1,0\Omega *{l_2}$$[/tex]

[tex]$$9,0v + 6,0v = 6,0\Omega *{l_2} + 6,0\Omega *{l_3} + 1,0\Omega *{l_2}$$[/tex]

[tex]$$9,0v + 6,0v = 7,0\Omega *{l_2} + 6,0\Omega *{l_3}$$[/tex]

_________________________________


Vi omskriver den andre likningen ved å bruke kirschoffs første lov:

[tex]$$ - 9,0v = - 6,0\Omega *\left( {{l_2} + {l_3}} \right) - 3,0\Omega *{l_3}$$[/tex]

[tex]$$ - 9,0v = - 6,0\Omega *{l_2} - 6,0\Omega *{l_3} - 3,0\Omega *{l_3}$$[/tex]

[tex]$$9,0v = 6,0\Omega *{l_2} + 9,0\Omega *{l_3}$$[/tex] (her trakk jeg sammen og ganget med -1)

_________________________________

1. [tex]$$7,0\Omega *{l_2} + 6,0\Omega *{l_3} = 15v$$[/tex]

2. [tex]$$6,0\Omega *{l_2} + 9,0\Omega *{l_3} = 9v$$[/tex]

Kalkulatoren løser disse likningene med to ukjente for oss (vi kan også gjøre dette med regning, ved å bruke innsettingsmetoden)

[tex]$$3,0A \wedge - 1,0A$$[/tex]

Grunnen til at vi får svaret [tex]$$ - 1,0A$$[/tex] er at strømmen i virkeligheten går omvendt retning av hva vi regnet med.

Vektormannen wrote:Kan du klare å finne den siste ligningen selv?

Først og fremst, en kjempe takk for en flott tilbakemelding!

Var mitt i føringen når du postet dette innlegget, så fikk ikke prøvd meg. Det jeg postet var det læreren som gjorde i timen, ville bare vise dere det.

Hvis jeg tar utgangspunkt i den likningen du fant:

[tex]$$3,0\Omega {I_3} + 6,0\Omega {I_1} + 9,0v = 0$$[/tex]

Så kan den andre feks være (høyre krets):

[tex]$$ - 3,0\Omega {I_3} + 1,0\Omega {I_2} + 6,0v = 0$$[/tex]

Eller hele kretsen (samme som ble brukt i den andre utregningen):

[tex]$$6,0\Omega *{l_1} + 9,0v + 1,0\Omega *{l_2} + 6,0v = 0$$[/tex]

Korrekt?

Det ser korrekt ut ja!

Vektormannen wrote:Det ser korrekt ut ja!

Tøft, skal se om jeg klarer neste oppgave her også da!

Forresten, når man ser på en oppgave (som er en krets). Er det riktig av hvis kretsen inneholder mer enn 1 spenningskilde, er man nødt til å ta i bruk kirschoffs lover for å beregne strømmen?

Hvis det hadde kun vært 1 spenningskilde, hadde det holdt med å regne ut resultantresistansen og bruke ohms lov for omgjøring?

(syntes nemlig jeg hørt læreren sa det)

Ja, hvis det hadde vært bare én spenningskilde i denne kretsen så kunne du ha funnet ut strømmene enklere, siden resistansen er kjent og du da bare får en "vanlig" parallellkobling. Det går kanskje an å resonnere seg frem til et svar selv når spenningskilden er med, men det man gjør da vil nok i bunn og grunn blir det samme som man får om man bruker Kirchoffs lover.