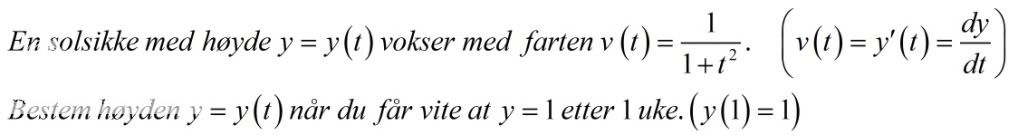matematikk.net

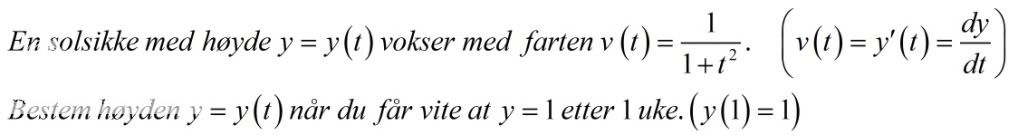Jeg forsøker: Jeg kan derivere farten for å finne ut hvor fort den vokser. Det de vil jeg skal gjøre er å besteme start høyden.

Sliter litt med å forstå sammenhengen her; kunne noen i det minste slengt ut hva de mener det spørres etter her? Det er jo en grei start å forstå.

Den deriverte av strekningen er farten

Så den integrerte av farten blir ?

Razzy wrote: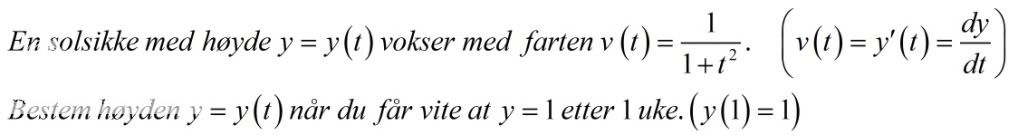

Jeg forsøker: Jeg kan derivere farten for å finne ut hvor fort den vokser. Det de vil jeg skal gjøre er å besteme start høyden.

Sliter litt med å forstå sammenhengen her; kunne noen i det minste slengt ut hva de mener det spørres etter her? Det er jo en grei start å forstå.

Som Nebu... skrev, integrer farten for å finne høyden.

Starthøyden er y(0)=... , er det den du blir spurt etter i oppgaven?

Svar: Nei, oppgaven spør etter y(t), som er uttrykket for høyden til solsikken. Dette finner du ved å integrere uttrykket for v, og så sette y(1)=1 for å finne verdien av integrasjonskonstanten C.

Kjør på med dette!

mstud wrote:

Razzy wrote: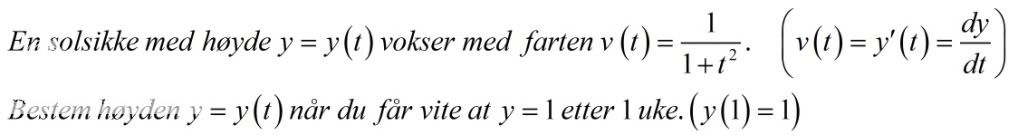

Jeg forsøker: Jeg kan derivere farten for å finne ut hvor fort den vokser. Det de vil jeg skal gjøre er å besteme start høyden.

Sliter litt med å forstå sammenhengen her; kunne noen i det minste slengt ut hva de mener det spørres etter her? Det er jo en grei start å forstå.

Som Nebu... skrev, integrer farten for å finne høyden.

Starthøyden er y(0)=... , er det den du blir spurt etter i oppgaven?

Svar: Nei, oppgaven spør etter y(t), som er uttrykket for høyden til solsikken. Dette finner du ved å integrere uttrykket for v, og så sette y(1)=1 for å finne verdien av integrasjonskonstanten C.

Kjør på med dette!

Løsningsforslag:


[tex]$$v\left( t \right) = \int {{1 \over {1 + {t^2}}}} \;dt$$[/tex]

[tex]$$y\left( t \right) = \arctan t + C$$[/tex]

[tex]$${\rm{Vi vet at:}}\;y\left( 1 \right) = 1$$[/tex]

[tex]$$\arctan 1 + C = 1$$[/tex]

[tex]$${\pi \over 4} + C = 1$$[/tex]

[tex]$$C = 1 - {\pi \over 4} \approx 0,215$$[/tex]

[tex]$$\underline{\underline {y\left( t \right) = \arctan t + 0,215}} $$[/tex]

Enige folkens?

Er det noen som er enige i løsningsforslaget jeg har lagt ut ovenfor? Det er jo en funksjon de spør etter, en funksjon avhengig av tiden-t.

Det ser helt riktig ut for meg i alle fall, med unntak av en liten slurvefeil øverst. Du mener vel y(t) på venstre side.

Vektormannen wrote:Det ser helt riktig ut for meg i alle fall, med unntak av en liten slurvefeil øverst. Du mener vel y(t) på venstre side.

Hei Vektormannen! Ja jeg mener y på V.S øverst Takk!

Da er jeg et steg nærmere en god eksamen

Razzy wrote:

Vektormannen wrote:Det ser helt riktig ut for meg i alle fall, med unntak av en liten slurvefeil øverst. Du mener vel y(t) på venstre side.

Hei Vektormannen! Ja jeg mener y på V.S øverst Takk!

Da er jeg et steg nærmere en god eksamen

Jeg er enig jeg også... du kunne selvfølgelig ha skrevet arctan(t) og arctan(1), for pyntens skyld... men det er jo en bagatell.

Likte i grunnen ganske godt arctant i ett ord, for det er mer humoristisk...

mstud wrote:

Razzy wrote:

Vektormannen wrote:Det ser helt riktig ut for meg i alle fall, med unntak av en liten slurvefeil øverst. Du mener vel y(t) på venstre side.

Hei Vektormannen! Ja jeg mener y på V.S øverst Takk!

Da er jeg et steg nærmere en god eksamen

Jeg er enig jeg også... du kunne selvfølgelig ha skrevet arctan(t) og arctan(1), for pyntens skyld... men det er jo en bagatell.

Likte i grunnen ganske godt arctant i ett ord, for det er mer humoristisk:


Rebus: hva er p*arctant*e ...

parctante ... Et ord jeg aldri har tenkt over at ligner såå mye på
arctan(t)...

Du tenker og du tenker, hehe

Skal passe på føringen! hehe

Razzy wrote:

mstud wrote:

Razzy wrote: Hei Vektormannen! Ja jeg mener y på V.S øverst Takk!

Da er jeg et steg nærmere en god eksamen

...

Du tenker og du tenker, hehe

Skal passe på føringen! hehe

Jasså, jeg tenker :p

Forhåpentligvis to steg nærmere en god eksamen ...