Er dette riktig definisjon av komplekse tall
[tex]\sqrt{-a}[/tex] (I)
Siden
[tex]\sqrt{ab}=y[/tex]
[tex]ab=y^2[/tex]
[tex]\sqrt{a}\sqrt{b}=z[/tex]
[tex]\sqrt{a}\sqrt{b}\sqrt{a}\sqrt{b}=z^2[/tex]
[tex]\sqrt{a}\sqrt{a}\sqrt{b}\sqrt{b}=z^2=ab=y^2[/tex]
[tex]\sqrt{ab}=y=z=\sqrt{a}\sqrt{b}[/tex]
får vi (I) til å bli:
[tex]\sqrt{-a}=\sqrt{-1}\sqrt{a}[/tex]
Vi kaller
[tex]i=\sqrt{-1}[/tex]
og får
[tex]\sqrt{-a}=i\sqrt{a}[/tex]
komplekse tall
Moderators: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa
Skjønner ikke hva du driver med jeg
hvor kom f.eks.
[tex]\sqrt{ab} = yab = y^2[/tex]
fra?
Hvis du skal vise at [tex]\sqrt{-a} = ai[/tex], så vil vel følgende, kjappe utledning motivere likheten nok.
[tex]\sqrt{-a} = \sqrt{a(-1)} = \sqrt{a}\sqrt{(-1)} = ai[/tex]
I grunnen er det vel mer et definisjonsspørsmål, siden kvadratrotfunksjonen i utgangspunktet kun er definert for ikke-negative reelle tall.
hvor kom f.eks.
[tex]\sqrt{ab} = yab = y^2[/tex]
fra?
Hvis du skal vise at [tex]\sqrt{-a} = ai[/tex], så vil vel følgende, kjappe utledning motivere likheten nok.
[tex]\sqrt{-a} = \sqrt{a(-1)} = \sqrt{a}\sqrt{(-1)} = ai[/tex]
I grunnen er det vel mer et definisjonsspørsmål, siden kvadratrotfunksjonen i utgangspunktet kun er definert for ikke-negative reelle tall.
Bachelor i matematiske fag NTNU - tredje år.
Å definere noe er jo akkurat det samme som å gi noe navn, så
[tex]i = \sqrt{-1}[/tex]
er både en navngivning og en definisjon.
Hvis [tex]y^2 = z^2[/tex] der y og z er reelle tall, trenger ikke nødvendigvis y og z være like hverandre. Se bare på y = 3 og z = (-3). Her er både y^2 = 9 og z^2 = 9, men y [symbol:ikke_lik] z.
[tex]i = \sqrt{-1}[/tex]
er både en navngivning og en definisjon.
Hvis [tex]y^2 = z^2[/tex] der y og z er reelle tall, trenger ikke nødvendigvis y og z være like hverandre. Se bare på y = 3 og z = (-3). Her er både y^2 = 9 og z^2 = 9, men y [symbol:ikke_lik] z.
Bachelor i matematiske fag NTNU - tredje år.
Å ja der skjønte jeg hva du mente jasvinepels wrote:Skjønner ikke hva du driver med jeg
hvor kom f.eks.
[tex]\sqrt{ab} = yab = y^2[/tex]
fra?
Har retta det opp nå. Manglet en ny linje skal bli
[tex]\sqrt{ab} = y[/tex]
[tex]ab = y^2[/tex]
ærbødigst Gill
Beviset mitt er ikke gyldig og viser ikke atsvinepels wrote:
Hvis [tex]y^2 = z^2[/tex] der y og z er reelle tall, trenger ikke nødvendigvis y og z være like hverandre. Se bare på y = 3 og z = (-3). Her er både y^2 = 9 og z^2 = 9, men y [symbol:ikke_lik] z.
[tex]\sqrt{ab}=\sqrt{a}\sqrt{b}[/tex]
p.g.a. det du skriver. Hvordan viser man det da?
EDIT
Dette fungerer bedre trur eg:
http://www.viewdocsonline.com/document/atec7t
Last edited by gill on 20/01-2012 19:06, edited 2 times in total.
ærbødigst Gill
La [tex]\sqrt{a}=x[/tex] og [tex]\sqrt{b}=y[/tex]. Da er [tex]a=x^2[/tex] og [tex]b=y^2[/tex], og [tex]ab=x^2y^2 = (xy)^2[/tex]. Dette gir at
[tex]\sqrt{ab} = \sqrt{(xy)^2} = xy = \sqrt{a}\sqrt{b}[/tex]
[tex]\sqrt{ab} = \sqrt{(xy)^2} = xy = \sqrt{a}\sqrt{b}[/tex]
Bachelor i matematiske fag NTNU - tredje år.
-
Per Spelemann
- Dirichlet

- Posts: 164
- Joined: 08/01-2012 01:48
Fikk lyst til å slenge inn en kommentar:
De reelle tallene kan vi si at danner ei tallinje.
De komplekse tallene kan vi si at danner et tallplan.
Se gjerne:
http://www.matematikk.net/ressurser/per ... hp?aid=167
De reelle tallene kan vi si at danner ei tallinje.
De komplekse tallene kan vi si at danner et tallplan.
Se gjerne:
http://www.matematikk.net/ressurser/per ... hp?aid=167
Per Spelemann wrote:Fikk lyst til å slenge inn en kommentar:
De reelle tallene kan vi si at danner ei tallinje.
De komplekse tallene kan vi si at danner et tallplan.
Se gjerne:
http://www.matematikk.net/ressurser/per ... hp?aid=167
Hvorfor skriver man komplekse tall i et plan?
EDIT:
Ser at uten plan kan man ikke finne lengden av komplekse tall men hvorfor man setter dem i et plan skjønner jeg ikke
Last edited by gill on 20/01-2012 18:55, edited 1 time in total.
ærbødigst Gill
-
Nebuchadnezzar
- Fibonacci

- Posts: 5648
- Joined: 24/05-2009 14:16
- Location: NTNU
Les litt mer i boken din du =)
Matte 3 ?
Alle tall er komplekse. Et komplekst tall skrives på formen
[tex]z = a + bi[/tex]
der a er den reellle delen og b er den imaginære delen.
Eksempelvis er alle reelle tall også på denne formen, bare at den imaginære delen er null.
Et kompekst tall, kan ogs uttrykkes som en vektor. Dette gjør vi ved
å la den vertikale aksen være den imaginære delen, og den horisontale aksen være den reelle delen.
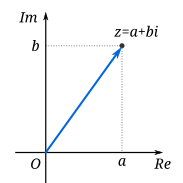
http://en.wikipedia.org/wiki/Complex_number
Men husk at dette bare er en definisjon av komplekse tall.
En annen definisjon er å konstruere ett nytt sett med tall, som tilfredstiller en del aksiomer eller regler. Som det står fint på wikipedia, under delen om matriser.
Matte 3 ?
Alle tall er komplekse. Et komplekst tall skrives på formen
[tex]z = a + bi[/tex]
der a er den reellle delen og b er den imaginære delen.
Eksempelvis er alle reelle tall også på denne formen, bare at den imaginære delen er null.
Et kompekst tall, kan ogs uttrykkes som en vektor. Dette gjør vi ved
å la den vertikale aksen være den imaginære delen, og den horisontale aksen være den reelle delen.

http://en.wikipedia.org/wiki/Complex_number
Men husk at dette bare er en definisjon av komplekse tall.
En annen definisjon er å konstruere ett nytt sett med tall, som tilfredstiller en del aksiomer eller regler. Som det står fint på wikipedia, under delen om matriser.
"Å vite hva man ikke vet er og en slags allvitenhet" - Piet Hein
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
https://s.ntnu.no/Integralkokeboken
Lektor - Matematikk, Fysikk og Informatikk
-
Per Spelemann
- Dirichlet

- Posts: 164
- Joined: 08/01-2012 01:48
Det finnes sikkert flere grunner til å skrive komplekse tall i et plan.
En grunn kan være at en geometrisk tolkning av de komplekse tallene gjør at kvadratroten av -1 ikke virker fullt så absurd.
En grunn kan være at en geometrisk tolkning av de komplekse tallene gjør at kvadratroten av -1 ikke virker fullt så absurd.
Altså ikke for å stille dumme spørsmål men i bunn og grunn ser det ut som dette er noe de bare gjør. Ser som sagt at etter at man har definert dette så kan man finne lengden ut fra planetNebuchadnezzar wrote:Les litt mer i boken din du =)
Matte 3 ?
Alle tall er komplekse. Et komplekst tall skrives på formen
[tex]z = a + bi[/tex]
der a er den reellle delen og b er den imaginære delen.
Eksempelvis er alle reelle tall også på denne formen, bare at den imaginære delen er null.
Et kompekst tall, kan ogs uttrykkes som en vektor. Dette gjør vi ved
å la den vertikale aksen være den imaginære delen, og den horisontale aksen være den reelle delen.
http://en.wikipedia.org/wiki/Complex_number
Men husk at dette bare er en definisjon av komplekse tall.
En annen definisjon er å konstruere ett nytt sett med tall, som tilfredstiller en del aksiomer eller regler. Som det står fint på wikipedia, under delen om matriser.
ærbødigst Gill
Ved å skrive komplekse tall i et plan får vi produktet av to tall på en meget fin form. Skriv tallene på polar form istedet for kartesisk form. Da vil produktet av komplekse tall gå ut på å multiplisere radiene og legge sammen vinklene.
Det er forsåidt ikke noe spesiellt med planet som gjør komplekse tall mulige.
La for eksempel [tex]Z=\left(\begin{matrix} a & b \\ -b & a\end{matrix}\right)[/tex] og [tex]W=\left(\begin{matrix} c & d \\ -d & c\end{matrix}\right)[/tex]. Da tilsvarer Z og W hhv. a+bi og c+di. Produkt av komplekse tall erstattes av matrisemultiplikasjon, og kompleks konjugasjon erstattes av transponering av matriser.
Prøv å beregne [tex]ZW[/tex] og [tex]ZZ^T[/tex] og se om du kjenner igjen resultatene.
Det er forsåidt ikke noe spesiellt med planet som gjør komplekse tall mulige.
La for eksempel [tex]Z=\left(\begin{matrix} a & b \\ -b & a\end{matrix}\right)[/tex] og [tex]W=\left(\begin{matrix} c & d \\ -d & c\end{matrix}\right)[/tex]. Da tilsvarer Z og W hhv. a+bi og c+di. Produkt av komplekse tall erstattes av matrisemultiplikasjon, og kompleks konjugasjon erstattes av transponering av matriser.
Prøv å beregne [tex]ZW[/tex] og [tex]ZZ^T[/tex] og se om du kjenner igjen resultatene.
Jeg er ikke sikker på om jeg forstår spørsmålet. Produktet av to complekse tall er en definert operasjon, hverken mer eller mindre. Hvis du mener hvordan produktet ser ut i polare koordinater, er det slik:gill wrote:Hadde vært topp hvis du forklarte litt mer hvor produktet kom innespen180 wrote:Ved å skrive komplekse tall i et plan får vi produktet av to tall på en meget fin form
[tex]z_1z_2=r_1 e^{i\theta_1} r_2 e^{i\theta_2} = r_1r_2 e^{i(\theta_1+\theta_2)}[/tex]
Der [tex]e^{i\theta} = \cos\,\theta + i\sin\,\theta[/tex]
Som du ser blir radiene multiplisert og vinklene addert. Problemet med denne representasjonen er derimot as addisjon av komplekse tall er ganske tungvindt.


