Integral: lik grad i teller og nevner
Posted: 15/10-2015 11:56
Hei igjen! 
Sliter litt med å komme i gang på denne oppgaven..
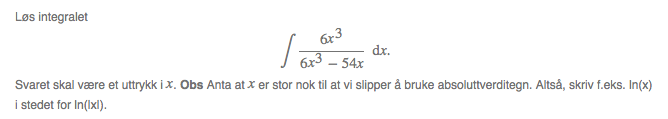
Slik jeg har forstått det, er man nødt til å utføre polynomdivisjon når ordenen er lik i teller og nevner, slik den er her. Her starter egentlig problemet mitt, for hvordan dividerer jeg disse med hverandre? Trodde jeg kunne dette, men står helt bom fast.
Men etter jeg har fått til polynomdivisjonen, skal man vel dele opp på vanlig måte, slik at jeg får
A/x + B/(x+3) + C/(x-3) (med 6 som konstant utenfor integralet) håper jeg?
Og deretter finne de ulike konstantene, og da blir jo integralet veldig greit!
Sliter litt med å komme i gang på denne oppgaven..
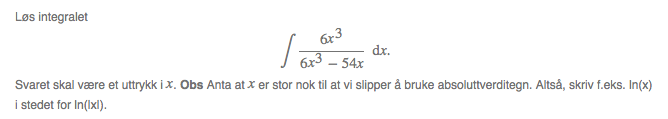
Slik jeg har forstått det, er man nødt til å utføre polynomdivisjon når ordenen er lik i teller og nevner, slik den er her. Her starter egentlig problemet mitt, for hvordan dividerer jeg disse med hverandre? Trodde jeg kunne dette, men står helt bom fast.
Men etter jeg har fått til polynomdivisjonen, skal man vel dele opp på vanlig måte, slik at jeg får
A/x + B/(x+3) + C/(x-3) (med 6 som konstant utenfor integralet) håper jeg?
Og deretter finne de ulike konstantene, og da blir jo integralet veldig greit!