Jeg har en prøve i R1 Algebra om ikke så alt for lenge og sitter derfor nå og gjør noen oppgaver vi fikk av læreren. Alt går veldig fint, bortsett fra en oppgave jeg ikke helt skjønner, som jeg håper noen kunne forklart meg. Oppgaven lyder som følgende:
Funksjonen f er gitt ved: [tex]f(x)=\frac{x^2+2}{x+1}[/tex].
a) Bruk polynomdivisjon til å skrive f(x) på en annen måte.
b) Tegn grafen til f. Velg x i intervallet [-4,6].
c) Hvilke to linjer nærmer grafen seg mot?
a oppgaven gikk veldig greit, men så kom b oppgaven. Jeg byttet ut x med alle verdiene [-4,6] og tegnet i et koordinatsystem:
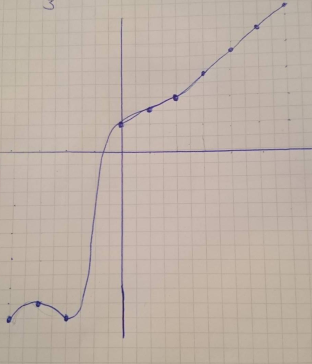
sjekket så svaret mitt med GeoGebra og fikk:
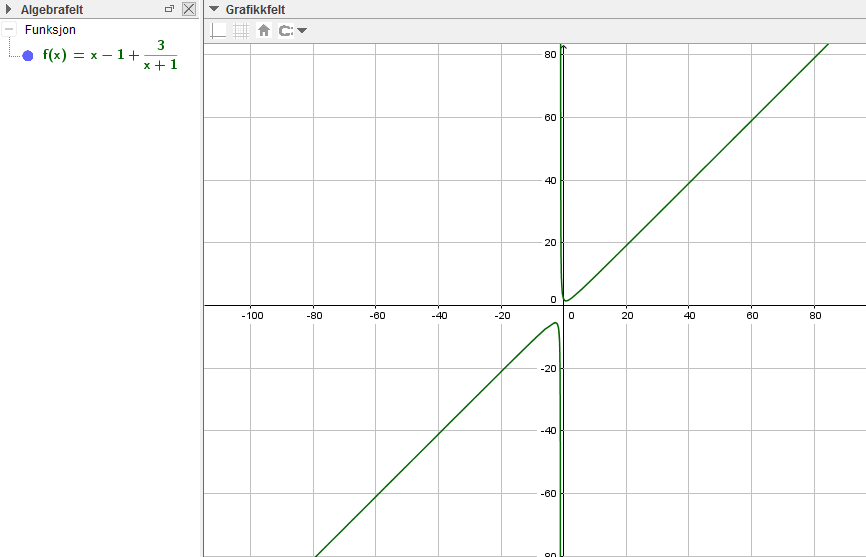
Det ser ut som jeg har gjort noe riktig, de to grafene på GeoGebra ligger på samme sted som min graf.
Det jeg ikke skjønner helt er hvorfor det er to grafer på GeoGebra? Hvordan kan jeg vite det, om dette er en Del 1 oppgave og jeg ikke får bruke GeoGebra?
Svaret på c er: Grafen nærmer seg asymptotene [tex]y_{a}=x+1[/tex] og [tex]x_{a}=1[/tex]. Hvis det trengs for en evt forklaring!
Takk på forhånd!


