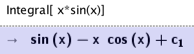Jeg har en integrasjonsoppgave der jeg ikke er helt enig med fasiten. Oppgaven er slik: finn integralet av x*sinx.
Jeg får x*cosx-sinx+C som svar, mens fasiten får x*cosx+sinx+C. Er det jeg eller fasiten som har rett?
Integrasjon
Moderators: Aleks855, Gustav, Nebuchadnezzar, Janhaa, DennisChristensen, Emilga
-
Fibonacci92
- Abel

- Posts: 665
- Joined: 27/01-2007 22:55
$(x \cdot cos x - sin x)^{\prime} = 1 \cdot cos x + x \cdot (-sinx) - cos x = - x \cdot sin x $
$(x \cdot cos x + sin x)^{\prime} = 1 \cdot cos x + x \cdot (-sinx) + cos x = 2cosx - x \cdot sin x$
Så ingen av dere har rett, men den ene er ganske nærme.
$(x \cdot cos x + sin x)^{\prime} = 1 \cdot cos x + x \cdot (-sinx) + cos x = 2cosx - x \cdot sin x$
Så ingen av dere har rett, men den ene er ganske nærme.
-
Dolandyret
- Lagrange

- Posts: 1264
- Joined: 04/10-2015 22:21
[tex]\int(x*sinx)dx[/tex], [tex]u=x[/tex], [tex]v'=sinx[/tex]stimorolextra wrote:Jeg har en integrasjonsoppgave der jeg ikke er helt enig med fasiten. Oppgaven er slik: finn integralet av x*sinx.
Jeg får x*cosx-sinx+C som svar, mens fasiten får x*cosx+sinx+C. Er det jeg eller fasiten som har rett?
bruker [tex]\int (uv')dx= uv-\int (u'v)dx[/tex]
[tex]-xcosx-\int(-cosx*1)dx=-xcosx+sinx+C=sinx-xcosx+C[/tex]
"I want to die peacefully in my sleep like my grandfather, not screaming in terror like his passengers."