Page 1 of 1
tilnærming
Posted: 02/11-2021 19:30
by seria
kunne jeg ha fått litt hint på oppgaven?
Re: tilnærming
Posted: 02/11-2021 19:58
by Aleks855
Har du funnet Taylorpolynomet?
Re: tilnærming
Posted: 02/11-2021 19:59
by Janhaa
Taylorpolynomet til cos(3x) finner du på linken under
…
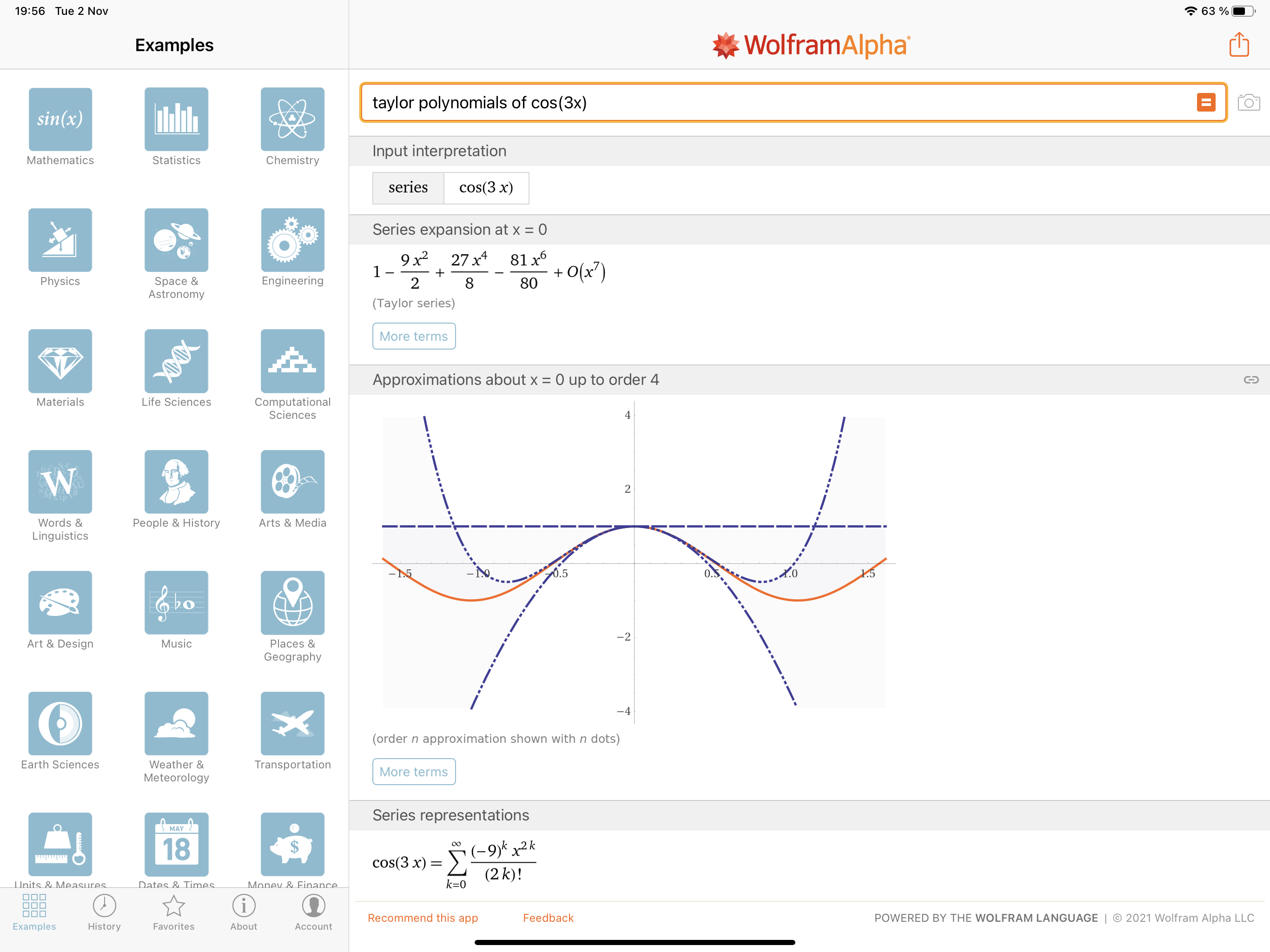
- 94798FEE-5496-45F6-B026-9F4EE3271DD8.png (826.83 KiB) Viewed 6389 times
Re: tilnærming
Posted: 02/11-2021 20:00
by Janhaa
Aleks855 wrote: 02/11-2021 19:58
Har du funnet Taylorpolynomet?
Sorry, så ikke du skrev dette… hjalp litt på vei..
Re: tilnærming
Posted: 05/11-2021 21:53
by seria
men hva gjør du etter det?
Re: tilnærming
Posted: 05/11-2021 22:06
by Aleks855
Du erstatter cosinus-uttrykket med dette polynomet, og løser likninga.
Re: tilnærming
Posted: 05/11-2021 22:33
by seria
skal jeg løse den taylorpolynom linknig? eller den likning fra oppgaven
Re: tilnærming
Posted: 06/11-2021 02:22
by Aleks855
1: Finn Taylorpolynomet av grad 2 for $\cos(3x)$
2: Bytt ut $\cos(3x)$ i likninga med polynomet fra steg 1
3: Løs den nye likninga.
Re: tilnærming
Posted: 08/11-2021 14:17
by seria
1-9x^2/2+27x^2/8-81x^6/80 +O(x^7)*1/4=6x er det slik, men hvordan regner man med O(x^7)
Re: tilnærming
Posted: 08/11-2021 15:30
by jos
Taylorpolynomet skal bare være av grad 2, altså bare de tre første leddene: $1 + 0 - 9\frac{x^2}{2} = 1 - 9\frac{x^2}{2}$
Re: tilnærming
Posted: 08/11-2021 17:49
by seria
jeg må lese denne liknigen: 1-9x^2/2
Re: tilnærming
Posted: 08/11-2021 18:49
by Janhaa
seria wrote: 08/11-2021 17:49
jeg må lese denne liknigen: 1-9x^2/2
[tex]6x=0,25(1-4,5x^2)[/tex]
Etc…