1P 2017 vår LØSNING
Løsning laget av matteprat-bruker knepz
Løsning laget av matteprat-bruker Lektor Nilsen
Løsning laget av Lektor Ørjan Augedal, Fana privat gymnas
DEL EN
Oppgave 1
15L = 150dL
$150 :2 = 75$
Jeg kan fylle 75 beger.
Oppgave 2
$\frac{1000 kr}{125} = \frac {x}{150} \\ x= \frac{1000kr \cdot 150}{125} \\ x= \frac{150000kr}{125} =1200$ kr
I 2016 koster våren 1200 kroner om den følger indeksen.
Oppgave 3
a)
x er celsius og y er fahrenheit.
$y = \frac{9}{5}x + 32 $
Setter x = 15 og får:
$y = \frac{9}{5} \cdot 15 + 32 \\ y=59 $
15 grader Celsius tilsvarer 59 grader Fahrenheit.
b)
$ x = \frac{9}{5}x + 32 \\ -\frac{4}{5}x = 32 \\ x = -40$
Det betyr at - 40C = - 40F. Legg merke til at vi byttet ut y med x, i forhold til oppgaven i a.
Oppgave 4
a)
| Personer | 1 | 2 | 3 | 4 |
| Pris per person | 780 | 390 | 260 | 195 |
b)
Personpris = $\frac{780}{antal \quad personer}$
Det koster 780 kroner til Gardermoen. Desto flere som er med på turen, desto flere blir det å dele regninga på. Når antall personer går opp, går stykkpris ned.
Oppgave 5
a)
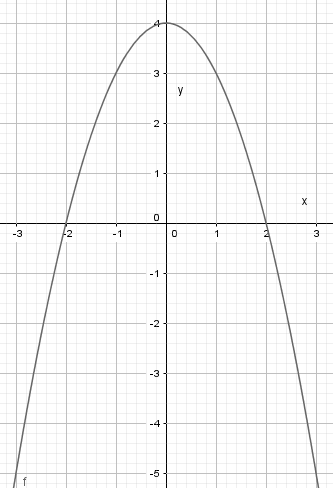
$f(x)=-x^2+4$
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | 0 | 3 | 4 | 3 | 0 | -5 |
b)
Du må tegne koordinatsystemet for hånd og merke av de syv punktene. Grafen skal være glatt, ingen knekkpunkter.
Oppgave 6
Sidene i kvadratetet er 12 meter.
Lengden av det korte katetet i trekanten blr da $\sqrt{13^2-12^2} = 5$ meter.
Lengden av rektangelet blir da 27 meter - 17 meter = 10m
AREAL:
A = trekant + kvadrat + rektangel + halvsirkel,
$A= \frac{5 \cdot 12}{2} + 12 \cdot 12 + 10 \cdot 4 + \frac{3 \cdot 2^2}{2} \\ 30 + 144 +40 + 6= 220 m^2$
Området har et areal på ca. 220 kvadratmeter.
OMKRETS:
Begynner med hypotenusen i trekanten og går mot klokka.
13m + 12m + 8m + 10m + 6m + 27m = 76m
Omkretsen er ca. 76 meter.
Oppgave 7
Startavgiften for å kjøre drosje er 65 kroner. I tillegg koster det 15 kroner per kilometer.
$f(x) = 15 x + 65 $, der x er antall kilometer,
Oppgave 8
a)
| Papir | Ikke papir | total | |
| Nett | 32 | 48 | 80 |
| Ikke nett | 18 | 2 | 20 |
| Total | 50 | 50 | 100 |
b)
Leser ut av tabellen i a at sannsynligheten for å lese både på nett og på papir er 32%
c)
$P( \bar{P} | N) = \frac{48}{80} = 0,6$
Det er 60% sannsynlig at vedkommende ikke leser papiraviser, gitt at han / hun leser nettaviser.
Oppgave 9
a)
Rødt og blått i forholdet 2 : 5.
$\frac{2}{5} = \frac{x}{7,5} \\ x = \frac{2 \cdot 7,5}{5} \\ x = 3$
Jeg trenger 3 dl rødmaling.
b)
Dersom vi blander i forholdet 2 : 5 består blandingen av 2 + 5 = 7 deler. Dersom vi trenger 21 liter ferdig blanding er en del 3 liter. Vi trenger da 6 liter rød o g 15 liter blå.
c)
1 : 3 er det samme som 2 : 6. I forhold til den tidligere blandingen som var 2 : 5, økes nå mengden blått. Vi trenger derfor å tilsette mere blå maling.
Det er 2 gange 3 liter rød maling i blandingen fra før. Jeg trenger en del blå maling til, altså må jeg tilsette 3 liter blå maling.
DEL TO
Oppgave 1
a)
b)
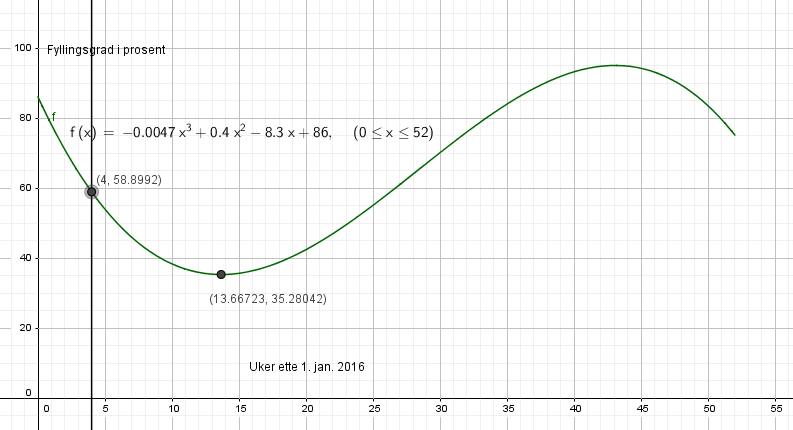
Bunnpunkt : (13.6 , 35.3). I uke 13 er fyllingsgraden på sitt laveste for året, ca. 35,3 %
c)
Prosentpoeng:
86 - 58,9 = 27,1
De fire første ukene ble vannstanden redusert med ca. 27,1 prosentpoeng.
Nedgangen i prosent var $\frac{27,1}{86} \cdot 100$% = 31,5%
Nedgangen var på ca. 31,5%.
Oppgave 2
Oppgave 3
Oppgave 4
Oppgave 5
Oppgave 6
Oppgave 7
Oppgave 8
a)
Gjør 90 km/h om til m/s $ \frac{90}{3,6}= 25$ m/s
På en mil bruker man 10000m / 25 m/s = 400 sek.
Deler 400 på 60 og får 6 minutter og en rest på 40 sekunder, altså tar det 6 min og 40 sek.