1T -H19-opg5
Fra Matematikk.net
Vi begynner med å legge inn funksjonen, finne nullpunkter og derivere:
a
Linje 3 gir oss nullpunktene x = 0 og x = k
b
Linje 4 gir oss den deriverte
c)
Fra linje 4 ser man at den deriverte er positiv når x = 0. Altså kan graf c passe til funksjonen.
d)
Setter den deriverte lik null og løser for x-verdiene. I linje 6 brukes "linje (punkt)(punkt)". Vi får likningen på uønsket form. Vi bruker "løs(....,y)" for å få den på en form der stigningstallet er lett å observere.
Stigningstallet til linjen gjennom ekstremalpunktene er $ \frac{-2k^2}{9}$.
e)
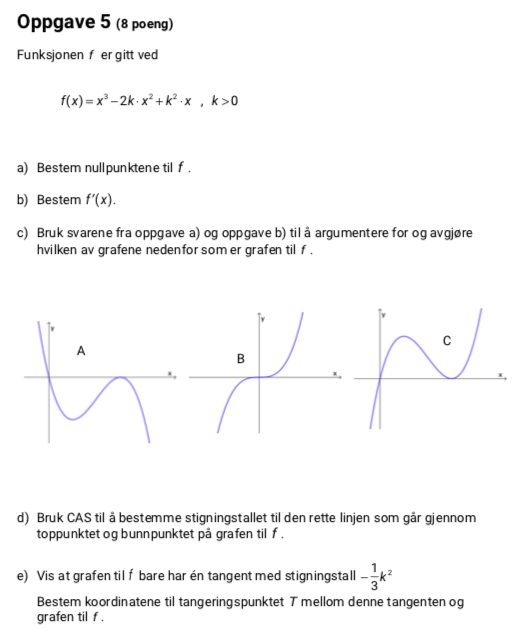
Vi finner koordinatene til tangeringen med stigningstall $- \frac{k^2}{3}$
Punkt: $( \frac{2k}{3}, \frac{2k^3}{27})$