2P 2014 høst LØSNING
DEL 1
Oppgave 1
$ \frac{0,0003 \cdot 500000000}{0,002}= \frac{3 \cdot 10^{-4} \cdot 5 \cdot 10^{8}}{2 \cdot 10^{-3}} = \frac{3 \cdot 5}{2} \cdot 10^{-4+8-(-3)} = 7,5 \cdot 10^7$
Oppgave 2
$x \cdot 1,25 = 250 \\ x = \frac{250}{1,25} \\ x =200$
Varen kostet 200 kroner før den ble satt opp.
Oppgave 3
300m = 30000cm
Vi vet at 500 ark er 6 cm. Dersom vi deler 30000 på 6 finner vi antall bunker med 500 ark. Så ganger vi med 500 for å finne antall ark.
$ \frac{30000}{6} \cdot 500 = \frac{3 \cdot 10^4 \cdot 5 \cdot 10^2}{6 \cdot 10^0 } = 2,5 \cdot 10^6$
I en 300 meter høy bunke med ark vil det være 2 500 000 ark
Oppgave 4
$\frac{2^3 \cdot 2^0}{2} - 8 \cdot 2^{-2} = \\ 2^{3+0-1} - 2^3 \cdot 2^{-2} =\\ 4 - 2 = 2$
Oppgave 5
a)
Det er 15 år mellom 2014 0t 2029. I denne perioden minker elevtallet med 350 - 275 = 75 elever, dvs. 5 elever per år. En lineær modell blir da:
y = -5x + 350 , der x er antall år etter 2014. y er antall elever et gitt år.
b)
Elever i 2024, dvs. x= 10:
$ y = -5 \cdot 10 + 350 = 300$
Etter modellen i a vil det være ca. 300 elever.
c)
I 2014 er elevtallet 200.
Det forventes en årlig vekst i elevtallet på 3%, derfor vekstfaktor 1,03.
x er antall år etter 2014.
Oppgave 6
a)
$L(3) = 1500 \cdot 1,08^3$
1500 er startverdi.
1,08 er vekstfaktor for 8%.
3 er perioder fram i tid.
b)
$L(juli, august, september, oktober) = 1500 \cdot 1,08^{-2}+1500 \cdot 1,08^{-1} + 1500 \cdot 1,08^0 + 1500 \cdot 1,08^1$
Oppgave 7
a)
y aksen viser frekvens delt på klassebredde. 1,5. Klassebredden er 50 - 30 = 20. Vi får da:
$ \frac{x}{20} =1,5 \\ x = 1,5 \cdot 20 \\ x=30$
b)
Ved å bruke samme metode som i a, på de tre andre klassene finner man at det var 100 personer på kinoen. 10 av disse er mellom 0-10 år. Prosent er del av hundre, dvs. 10%.
c)
Vi finner antall personer i hver klasse, og antar at aldersfordelingen innen hver klasse er jevnt fordelt rundt klassemidtpunket.
| Klasse | Klassemidtpunkt, x | Antall personer, n | $n \cdot x$ |
| 0 - 10 | 5 | 10 | 50 |
| 10 - 30 | 20 | 40 | 800 |
| 30 - 50 | 40 | 30 | 1200 |
| 50 - 90 | 70 | 20 | 1400 |
| Sum | 100 | 3450 |
Gjennomsnittsalderen blir da $3450 : 100 = 34,5$ år, under forutsetning av at antakelsen vår er riktig.
Oppgave 8
a)
Torbjørn kom først til Torsøy. Han er der en halv time. Tore kom ti minutter senere. Han er der i 20 minutter.
b)
Tore holder konstant fart. Han bruker 40 minutter på 4 km. Det tilsvarer 1 km på 10 minutter. Det er 6 ti-minuttere i en time, dvs. farten er 6 km / time.
c)
De starter tilbaketuren samtidig. Tore padler med konstant fart og kommer fram 10 minutter før Torbjørn. Torbjørn padler raskt de første fem minuttene, 12 km / time, men har så fem minutter pause.
Oppgave 9
a)
Det spilles 16 kamper: Det skåres i gjennomsnitt:
$\frac{0\cdot 2 +1 \cdot 6+ 2 \cdot 3 + 3\cdot 4 + 4 \cdot 1 }{16} = \frac{28}{16} = 1,75 $
Oda skårer i gjennomsnitt 1,75 mål per kamp.
Det er 16 kamper totalt. Dette er et partall så da vet vi at det er 2 tall i midten. Disse tallene kan finnes på denne måten:
$\frac{16}{2}=8 $
Dette betyr at tall nummer 8 og 8+1=9 er de to tallene som skal benyttes for å regne ut medianen. For 0 mål har vi 2 kamper, for 1 mål har vi 6 kamper. Det vil si at tall nummer 8 er i gruppen med 1 mål. Tall nummer må da være i raden med 2 mål. Tall nummer 8 er altså 1, og tall nummer 9 er 2.
Median = $\frac{1 + 2}{2} = 1,5 $ mål
b)
Den kumulative frekvensen for to mål er 11 ( 2 + 6 + 3). Det betyr at i 11 kamper skårer hun 2 mål eller mindre.
c)
Frekvensen for 3 mål er 4. Da er den relative frekvensen for 3 mål $ \frac{4}{16} = \frac{1}{4}$
d)
Hun skårer 4 mål i 25% av kampene. I 11 av 16 kamper skårer hun to mål eller mindre.
DEL 2
Oppgave 1
a)
Fra Excel får man:
23,5
26,1
18,4
22,8
25,1
20,3
22,7 Gjennomsnitt
2,652671609 Standardavvik
Gjennomsnittskastet er 22,7 meter, med et standardavvik på 2,65 meter.
b)
Hvem som er best kan vi ikke si noe om, men Sven kaster jevnere på lengdene enn Kjell, som har et standardavvik på 3,2 m.
Oppgave 2
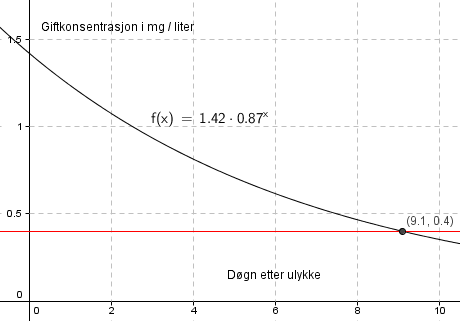
$f(x)= 1,42 \cdot 0,87^x$
a)
Rett etter ulykken er x=0, dvs. giftkonsentrasjonen er 1,42 mg / L.
Giftkonsentrasjonen minker med 1 - 0,87 = 0,13 = 13% per døgn.
b)
Gjennomsnittlig nedgang per døgn:
Rett etter ulykken: 1,42 mg /L.
Syv døgn etter ulykken: $ f(7)= 1,42 \cdot 0,87^7 = 0,54$ mg/L.
Gjennomsnitt per døgn (de første syv): $\frac{0,54 - 1,42}{7 } \approx -0,13$ mg/L.
Nedgangen var på ca 0,13 mg/liter i gjennomsnitt per døgn, de første syv døgn.
c)
Etter 9,1 dager er giften nede på 0,4 mg /L. Det kan nok være fornuftig å vente til dag 10 etter ulykken før man begynner å drikke det.
Oppgave 3
a)
Etter 10 år har Mads: $f(10)= 25000 \cdot 1,0225^{10} = 31230,09$ kroner i banken.
Prosentvis er dette en økning på $\frac{31230,09}{25000} =1,2492 \approx 24,92$ %
b)
Ti år etter konfirmasjonen har Malin $((25000 \cdot 1,0225^5)+ 25000)1,0225^5 = 59172,03 $ kroner på konto.
Oppgave 4
a)
b)
Modellen blir slik ut fra figuren:
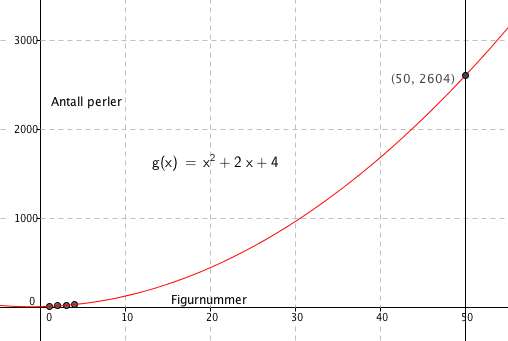
$F_n= n^2+2n+4 $
c)
Man leser Fra figuren at $F_{50} = 2604$. Ved utregning bruker man funksjonsuttrykket i b og får
$F_{50} = 50^2+2 \cdot 50 +4 = 2604$
Man trenger altså 2604 perler for å lage figur nummer femti.
Oppgave 5
a)
Overflate = 2 kortsider + forside + tak
$O(x)= 2 \cdot h \cdot x + 4 \cdot h \cdot x + 4 \cdot x \cdot x \\ O(x)= 2hx+4hx+4x^2 \\ O(x)= 4x^2+6hx$
b)
Vi får beskjed om at O(x) = 40. Skal få h alene på venstre side.
$40 = 4x^2+6hx \\ 40 - 4x^2 = 6hx \\ 6hx= 40-4x^2 \\ h = \frac{40-4x^2}{6x} $
c)
En slik kasse kalles et prisme. Volumet av et prisme er
$V= Gh \\ V(x) = 4x^2h$
Nå har vi to variabler, x og h. Vi bytter h med uttrykket vi fant i b og får:
$V(x)= 4x^2 \cdot \frac{40-4x^2}{6x} \\V(x)= - \frac 83x^3+ \frac{80}{3}x $
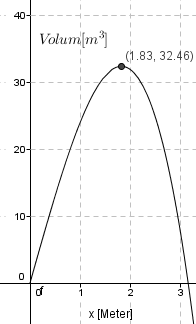
Vi setter så funksjonsuttrykket inn i Geogebra og ser hvordan volumfunksjonen ser ut.
Vi observerer at volumet er størst når x = 1,83 meter. Da er volumet 32,46 $m^3$. det betyr at buret må være 1 meter og 83 centimeter dypt. Lengden skal ganges med fire, så lengden blir 7,32 meter.
Høyden på buret er gitt i b: $ h = \frac{40-4x^2}{6x} $. Det gir en høyde på 2,42 meter, når vi setter inn 1,83 for x. Da gjenstår det bare å kjøpe fuglene ,-)
Oppgave 6
a)
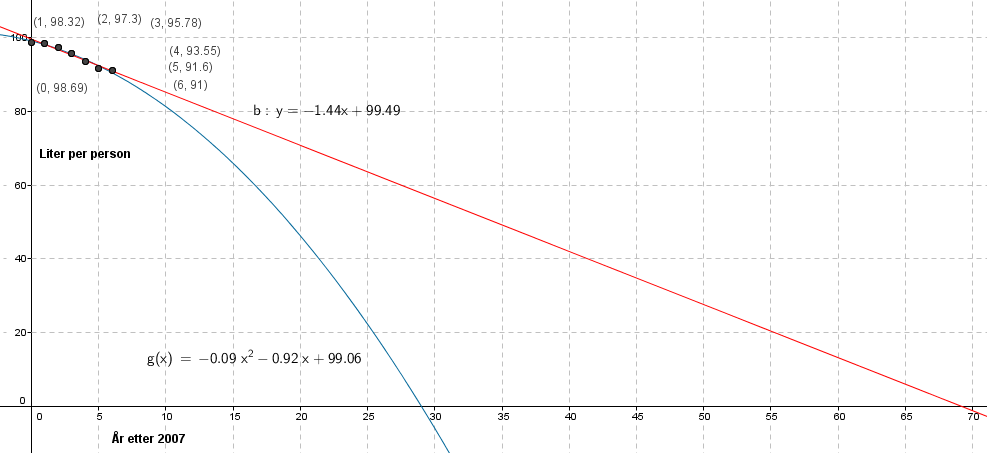
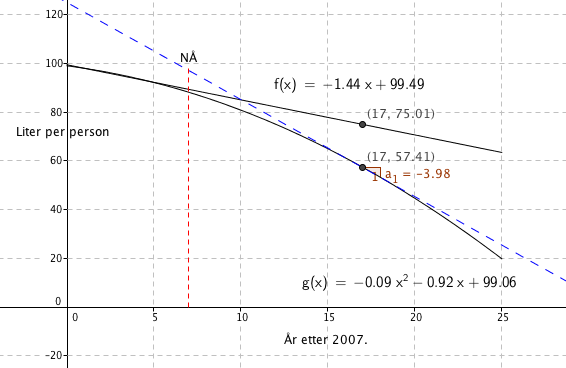
Det har vært en nedgang i forbruket av melk, fra 2007 til 2013. Basert på de tre siste årene ser det imidlertid ut til at nedgangen er i ferd med å stagnere. Tallet for 2014 er 89,67 liter (melk.no) så min antakelse i setningen over støttes ikke. Den lineære modellen er trolig den mest realistiske. Andregradspolynomet gir en dramatisk utvikling, der man slutter å drikke melk før 2037. Ingen av modellen er trolig realistiske i et langt tidsperspektiv.
b)
c)
Fra figuren i b ser man at den lineære modellen gir 75,0 liter per person, mens polynom modellen gir 57,4 liter per person.
d)
Leser av Figuren i b:
Om 10 år avtar forbruket med
1,44 liter per år, etter lineær modell og med
4 liter per år, etter polynom modellen.
Oppgave 7
a)
Båndet er 3,25 meter langt. For a finne den reelle farten ganger man antall runder med 3,25 og deler på 60. Da har man farten i meter per sekund. Ved å gange med 3,6 får man farten i kilometer per time.
Reell fart$= \frac{Runder \cdot 3,25 \cdot 3,6}{60} = 0,195 \cdot Runder$
| Angitt fart
x, km/h |
Antall runder i
løpet av ett minutt |
Reell fart
f(x) km/h |
| 2,5 | 18 | 3,51 |
| 5,0 | 35 | 6,83 |
| 10,0 | 65 | 12,68 |
| 15,0 | 95 | 18,53 |
| 20,0 | 124 | 24,18 |
b)
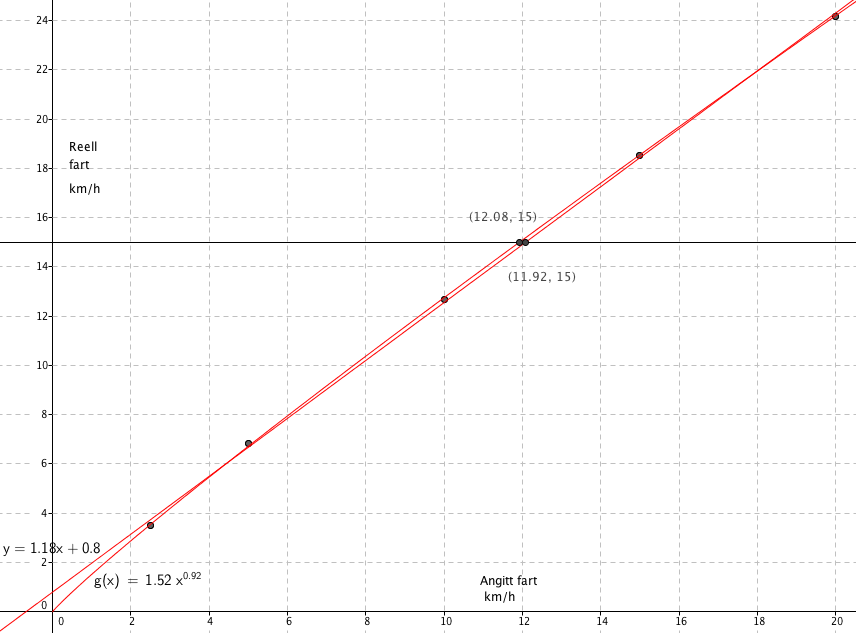
Lineær modell: $ y(x)=1,18x+ 0,8$
Potens modell: $ g(x)= 1,52x^{0,92}$
Potensregresjonen har en ørliten bedre R verdi enn den lineære regresjonen. I tillegg starter potens modellen i origo, hvilket jo er riktig når møllen står stille. Man bør derfor velge den.
c)
Figuren i b viser at dersom han har lyst til å løpe 15 km/h så må møllen stilles på 12 km/h.
d)
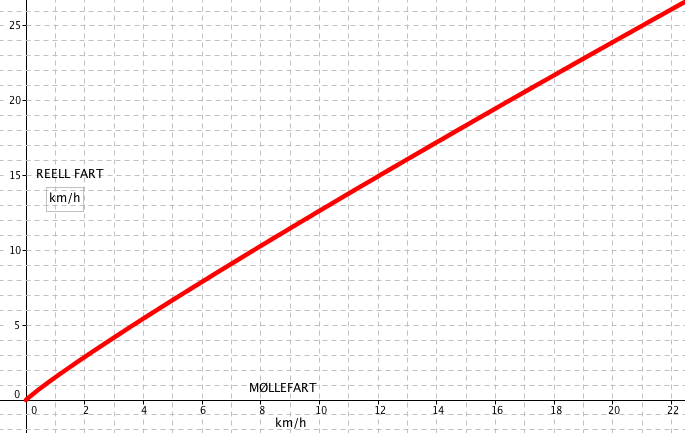
NB: Møllen viser for liten fart.
Her ser du sammenhengen mellom vist møllegart og reell fart.