2P 2021 Høst eksempel LK20 LØSNING
DEL EN
Oppgave 1
Ett parti øker oppsluttningen fra 5% til 7%. Det er en $\frac{2}{5}= \frac{4}{10} = 40$ % økning.
Oppgave 2
Programmet regner ut hvor lang tid det tar før verdien til en vare er halvert, når verdien avtar med 15% per år. Linje 10 skriver ut denne verdien og linje 11 skriver ut hvor lang tid det tar.
Oppgave 3
Dersom et produkt skal bli null, må en eller flere av faktorene være null.
Løsning: x = 0 eller x = 3 eller x = -1.
Oppgave 4
Vi kan finne høyden i trekanten ved å bruke Pytagoras. Den blir 8 cm. Normalen på AB gjennom C deler AB i to like store biter, fordi trekanten er likebeint. Vi finner da arealet av den rettvinklede trekanten som er halvparten av trekant ABC.
Arealet av trekanten blir da grunnlinje gange høyde delt på to, som er $24 cm^2$. Da har vi funnet arealet av halvparten av trekanten. Arealet av trekanten ABC blir da $A= 48 cm^2$
Oppgave 5
Det er høyden på arket som begrenser størrelsen på bildet. Vi bruker formlikhet:
$\frac{8}{28} = \frac{x}{42}$
$x= \frac{8 \cdot 42}{28} =12$
Bildet kan bli 42 cm høyt. Da blir det 12 cm i bredden.
Oppgave 6
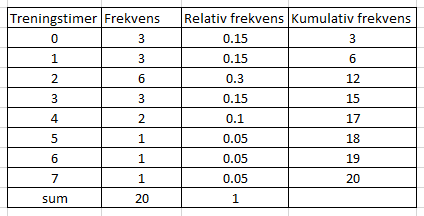
Vi kan bruke 2 treningstimer som eksempel. Frekvensen er 6. Den relative frekvensen forteller hvor mange timer 6 er av 20, altså 6/20 som er 0,3 eller 30%. Den kumulative frekvensen for 2 treningstimer er 12. Det betyr at 12 personer trene 2 timer eller mindre (3 + 3 + 6).
Oppgave 7
I et histogram representerer arealet av en enkelt søyle antallet eller frekvensen. Antallet elever som er under 180 cm høye blir summen av arealene som er under 180cm: 10 + 30 + 50 = 90 elever.
Oppgave 8
Begrunnelsen i oppgaven er riktig. $4x^2-2x+5$ er en "smilende" parabel som ligger over x- aksen. Ulikheten har derfor ingen løsning.
DEL TO
Oppgave 1
Synne har rett. Når noe minker med 4% er vekstfaktoren 0,96.
Thea, ja man kan bruke den vekstfaktoren. Siden verdien minker var den større for åtte år siden, enn i dag, så det har Thea rett i.
Dersom vi kaller båtens verdi for ått år siden for x får vi:
$x \cdot 0,96^{8} = 45000$
$x = 45000 \cdot 0,96^{-8}$
x= 62400
For åtte år siden var båtens verdi rundt 62 000 kroner. (ikke noe poeng å regne på krona her, dette er også en modell for verdiutviklingen og svaret er ikke eksakt uansett antall desimaler).
Oppgave 2
a)
b)
2,2 se figur i a.
c)
$112,2 - 93,3 = 18,9$ prosentpoeng som utgjør en $ \frac{18,9}{93,3} \cdot100 = 20,3$ %.
d)
Oppgave 3
a)
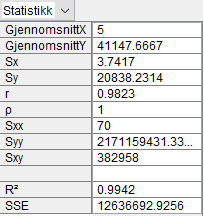
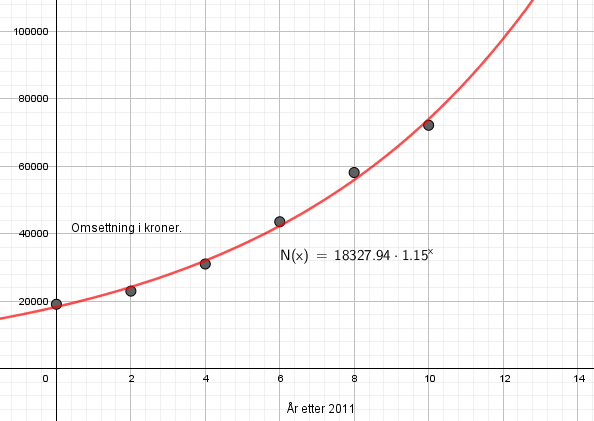
Brukte regresjon i Geogebra. Vi ser at N passer god til dataene fra 2011 til 2021. Kvadratet av regresjonskoeffisienten er 0,99 hvilket tyder på god tilpasning (jo nærmere 1 jo bedre tilpasning til målepunkter).
b)
Vekstfaktoren på 1,15 forteller at omsetningen øker årlig med ca. 15%.
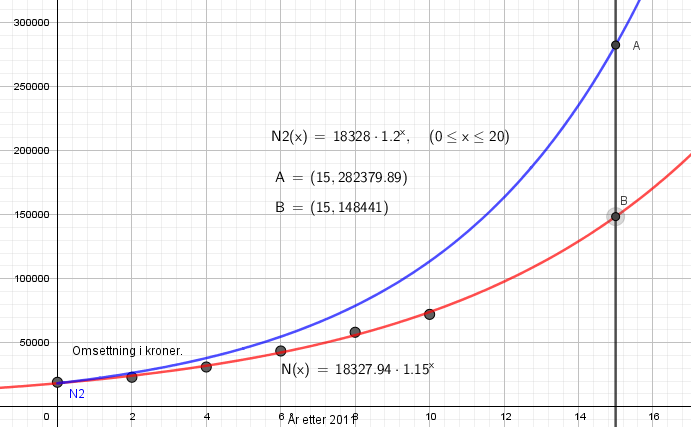
c)
Oppgave 4
Når vi beregner skattetrekk er det av bruttolønn minus pensjonsinnskudd og fagforeningskontingent. I denne oppgaven skal vi finne bruttolønna og må regne oss "bakover".
Vi finner først trekkgrunnlaget. 35% er betalt i skatt, så 38 456 kr utgjør 65%. Trekkgrunnlag $= \frac{38456kr \cdot 100}{65} = 59163 kr$
Vi legger til kr 723 som hun har betalt i fagforeningskontingent, og får 59 886 kr. Hun har betalt 2,5% i pensjonsinnskudd, så 59 886 kr utgjør 97,5% av bruttolønna. Den er: $\frac{59886 \cdot 100}{97,5} = 61 422 $kr.
Oppgave 5
a)
Blant 20 elever vil medianverdien være gjennomsnittet av elev nr. 10 og 11. (stigende rekkefølge ). Vi ser at medianen er 6 land.
Gjennomsnitt: $\frac{4 \cdot 3 + 5 \cdot 4 + 6 \cdot 5 + 8 \cdot 5 + 10 \cdot 2 + 50}{20} = 8,6$
b)
Vi ser at en elev har vært i 50 land. Den eleven trekker opp gjennomsnittet. Gjennomsnittet uten denne eleven er 6,4. Jeg tenker at medianverdien best beskriver datamateriealet.
Oppgave 6
a)
Gjennomsnittspris: $\frac{30 kr}{39,75 kWh} = 0,75$ kr/kWh.
b)
Vi ser at kraftforbruk og pris per enhet kraft er i samme diagram. Her brukes time 04 som eksempel på hva som er gjort. Søylen viser ca 3,3 kWh som multipliseres med 55 øre/kWh. Det blir 1,815 kroner, som er prisen for den timen. Vi gjør dette med timene fra 00 til og med 05 og får:
$1,2 \cdot 0,55 + 1,6 \cdot 0,55 + 1,8 \cdot 0,55 + 1,815 + 0,60 \cdot 1,4 =5,19$
De seks første timene kostet ca. 5,19 kroner.
Oppgave 7
a)
Dersom en sirkel skal ha et areal på $10cm^2$ får vi radius:
$10 = \pi \cdot r^2$
$r = \sqrt{\frac{10}{\pi}}= 1,78$
som gir en diameter på 3,57 cm.
b)
Arealet av en sirkel
$A= \pi r^2$
Dersom arealet skal øke med faktoren 1,44 hver gang får vi uttrykket:
$1,44 A =1,44 \pi r^2 = \pi (1,2 \cdot r)^2$
Man må øke radius med en faktor 1,2 for å øke sirkelens areal med en faktor 1,44.
Oppgave 8
Fredrik deler på x. Dersom x = 0 deler han på 0 og er ille ute å kjører. Dersom han ønsker å løse den algebraisk kan han gjøre slik
$x^2 \leq 3x$
$x^2-3x \leq 0$
$x( x-3) \leq 0$
Vi ser at uttrykket gir null for x=0 og x = 3. For å finne verdien mellom tester vi for x=1 og ser at uttrykket er negativt. Om man ikke ser det må man tegne fortegnsskjema.
Løsningsmengden for ulikheten blir da:
$x \in [0,3]$
Cecilie har valgt en grafisk løsning. Hun har tegnet inn $x^2$ og $3x$ i et koordinatsystem og gitt seg med det. Siden de fleste sensorer ikke har telepatiske evner er ikke dette nok. Hun må forklar hvilke funksjon og graf som hører sammen og at funksjonen 3x har en større eller lik verdi enn $x^2$ i området x = 0 til x = 3.
Min personlige vurdering er at ingen av besvarelsene var riktige men at Cecilie sin bare var mangelfull, mens Fredrik sin var feil (det kan sikkert diskuteres).
Oppgave 9
15% av 2 500 000 kr er 375 000 kr, så egenkapitalkravet oppfyller hun. Med en inntekt på 490 000 kr. kan maksimal total lånebelastning være 2 450 000 kr. Trekker vi fra studielånet som hun allerede har, kan hun låne 2 200 000kr. Sammen med egenkapitalen har hun nok penger til å kjøpe leiligheten.
Oppgave 10
I regnearket nedenfor blir du bedt om å skrive inn fartsgrensen på strekningen, hvor lang distanse du skal kjøre, og din planlagte gjennomsnittsfart på turen.
Dersom fartsgrensen er 80 km/h og du skal kjøre 12 km regner arket ut hvor mye du sparer i tid på 12 km med din planlagte gjennomsnittsfart, sammenlignet med en gjennomsnittsfart på 80 km/h.